Einführung und Fragestellung
Oft hat man in der Mathematik und besonders in Anwendungen der Mathematik mit Gleichungen zu tun, in denen Variablen vorkommen. Ist nur eine Variable vorhanden, möchte man deren Zahlenwert wissen; sind es mehrere Variablen, will man eine aus der anderen berechnen. Letzteres hat übrigens viel mit Funktionen in der Mathematik zu tun.
Zwei einfache Beispiele:
- 5 Amazon-Gutscheine kosten 100 €, wieviel kostet ein Gutschein? Als Formel (Kosten eines Gutscheins: x):
5·x = 100; wie groß ist x? - Ein Kilo Mehl kostet 2 € und ein Kilo Zucker 3 €. Ich will beides kaufen und insgesamt 10 € ausgeben. Wieviel Kilo Zucker (y) kann ich bekommen, wenn ich x Kilo Mehl kaufen will? Als Formel:
2·x + 3·y = 10; wie groß ist y, wenn ich x vorgebe?
Wir werden dem Geheimnis des Gleichungslösens in folgenden Abschnitten näher kommen:
Grundlegende Methodik
Ausgangspunkt ist immer eine Gleichung, in der eine oder mehrere Variablen vorkommen. Die Gleichung kann richtig oder falsch sein, je nachdem welchen Wert ich für die Variable einsetze. Gesucht ist der oder die Werte, bei denen die Gleichung wahr wird. Beispiel:
5·x = 10
Einsetzen von x=4 führt zu
5·4 = 20 ≠ 10; die Gleichung ist für x=4 falsch; x=4 ist keine Lösung der Gleichung
Probieren wir x=2:
5·2 = 10; die Gleichung ist für x=2 richtig; x=2 ist eine Lösung der Gleichung
Ausprobieren kann also zum wahren Wert der Variablen führen. Es kann aber bei komplexeren Geichungen ziemlich beschwerlich sein und lange dauern…
Wir brauchen also eine praktikablere Methodik, um die wahren x-Werte einer Gleichung zu finden. Dies ist das Auflösen der Gleichung nach der Variablen. Auflösen der Gleichung nach einer Variablen bedeutet, dass diese Variable nach irgendwelchen Operationen, die man auf beide Gleichungsseiten anwendet, allein auf einer Seite steht. Warum?
Wenn eine Gleichung wahr ist, steht links und rechts vom Gleichheitszeichen – wie eben gesagt – dasselbe. Macht man mit beiden Seiten das Gleiche (wendet man die gleiche Operation an), bleibt die Gleichung wahr. Beispiele:
In der Gleichung 5 = 2+3 wird auf beiden Seiten 6 addiert. Sieh‘ Dir im Video an, was passiert.
Es ergibt ich 11 = 11, was nach wie vor wahr ist.
Auch eine Multiplikation auf beiden Seiten ändert die Wahrheit der Gleichung nicht:
Übrigens: wichtig ist hier, dass die gesamte rechte Seite mit 6 multipliziert wird; deshalb die Klammern!
Durch geschickte Wahl der Operationen kann man eine Gleichung nach einer Variablen auflösen. Man muss dafür sorgen, dass die Variable nach und nach alleine auf einer Gleichungsseite verbleibt. Beispiel:
5·x = 10
Indem man beide Seiten durch 5 dividiert, steht rechts nur noch x und links 2. Einsetzen von x=2 in die Ursprungsgleichung zeigt: x=2 ist eine Lösung!
Zum Schluss des Methodenabschnitts noch die schrittweise Auflösung unserer anderen Beispielgleichung nach y (wieviel Mehl bekomme ich?) im Slider.
In der Ergebnisgleichung kann man für x irgendwelche Werte einsetzen:
- Wenn x=0, ist y=5 (wenn ich auf Zucker verzichte, bekomme ich 5 kg Mehl)
- Wenn x=2, ist y=2 (ich bekomme jeweils 2 kg Mehl und Zucker)
- Wenn x=10/3, ist y=0 (10 Drittel kg Zucker bedeuten: kein Mehl)
- Wenn x>10/3, dann wird y negativ (ich müsste also einen Kredit aufnehmen, um Mehl zu bekommen)
Welche Operation man wann am besten anwendet ist eine Frage der Erfahrung. Manche Gleichungen sind schwer zu durchschauen, bei anderen fällt einem der Lösungsweg direkt ins Auge. Zudem gibt es meistens mehrer Lösungswege.
Je mehr man Gleichungen selbst gelöst hat, desto zuverlässiger und schneller geht es. Wichtig ist allerdings, die Grundregeln des Rechnens zu beherrschen (z.B. Punktrechnung vor Strichrechung, ausklammern oder ausmultiplizieren etc.).
Lösbarkeit von Gleichungen
Bisher hatten wir Beispiele für Gleichungen, die recht einfach zu lösen sind. Es stellt sich die Frage, ob alle Gleichungen eine Lösung besitzen – also Variablenwerte gefunden werden können, die eine Gleichung wahr machen. Die Antwort ist einfach: nein!
Schon sehr simple Gleichungen haben keine Lösung, beispielsweise
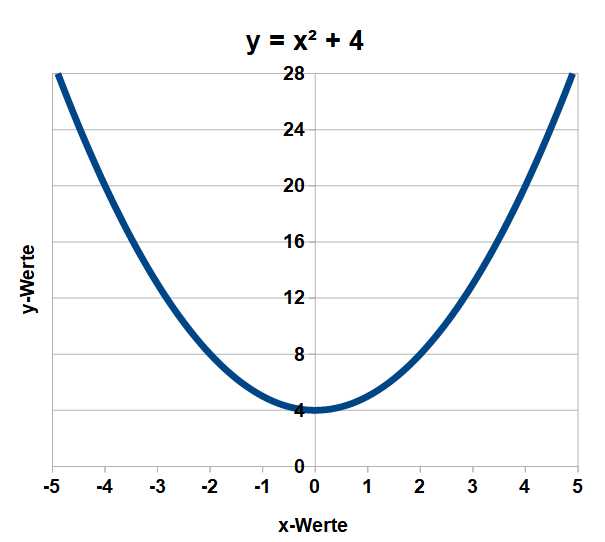
x² + 4 = 0
Wenn man auf beiden Seiten 4 subtrahiert, wird das zu
x² = -4
Um x – und nicht x² – zu erhalten, muss man die Quadratwurzel ziehen, also die Zahl finden, die mit sich selbst multipliziert -4 ergibt. Gemäß der Regel „minus mal minus ergibt plus“ bzw. „plus mal plus ergibt auch plus“ gibt es keine Zahl, die mit sich selbst multipliziert eine negative Zahl ergibt. Sprich: die Gleichung x² + 4 = 0 hat keine Lösung! Jedenfalls nicht, solange x eine relle Zahl ist.
Man kann sich dies klarmachen, wenn man x² + 4 = 0 als Spezialfall der Funktion y = x² + 4 für y = 0 betrachtet. Der Funktionsgraph dieser Funktion zeigt, dass y immer größer oder gleich 4 ist – egal welchen x-Wert man wählt! y kann also niemals Null sein.
Leider gibt es keine einfache Methode mit der man schnell sehen kann, ob eine Gleichung lösbar ist oder nicht. Klar ist aber: wenn man beim Auflösen auf einen Widerspruch in der Gleichung stößt oder es schlicht keine Zahl gibt, die die Gleichung wahr macht, ist sie nicht lösbar.
Gleichungstypen
Es gibt viele verschiedene Typen von Gleichungen. Beispiele:
Algebraische Gleichungen:
\[y(x)=a_0+a_1· x+a_2· x^2+…\]
Exponential-Gleichungen:
\[y(x)=a·e^{b x}\]
Trigonometrische Gleichungen:
\[y(x)=A·sin(2π·ν·x)\]
etc.
Die Operationen, die man zu ihrer Lösung benutzen kann, hängen eng mit dem Gleichungstyp zusammen. Für algebraische Gleichungen sind dies im Wesentlichen die Grundrechenarten und das Wurzelziehen. Bei den Exponentialfunktionen spielt zusätzlich der Logarithmus eine Rolle und bei trigonometrischen Funktionen die Umkehrfunktionen der Basisfunktionen Sinus, Cosinus, Tangens und Cotangens.
Übungsbeispiele
Zum Abschluss ein paar Übungsaufgaben mit Erläuterungen zum Lösungsweg:
Quiz:
Löse nach x auf
7x + 14 = 21
Klicke die richtige Lösung an:
Lösungsweg A:
- subtrahiere 14 (ergibt: 7x = 7)
- dividiere durch 7
Lösungsweg B:
- dividiere durch 7 (ergibt: x + 2 = 3)
- subtrahiere 2
Quiz:
Löse nach y auf
2y - 4x = 8
Klicke die richtige Lösung an:
Lösungsweg A:
- addiere 4x (ergibt: 2y = 8 + 4x)
- dividiere durch 2
Lösungsweg B:
- dividiere durch 2 (ergibt: y – 2x = 4)
- addiere 2x
Quiz:
Löse nach x auf
3x² -12 = 0
Klicke die richtige Lösung an:
Lösungsweg A:
- addiere 12 (ergibt: 3x² = 12)
- dividiere durch 3 (ergibt: x² = 4)
- ziehe die Quadratwurzel
Lösungsweg B:
- dividiere durch 3 (ergibt: x² – 4 = 0)
- addiere 4 (ergibt: x² = 4)
- ziehe die Quadratwurzel
Hinweis: beachte, dass die Quadratwurzel positiv und negativ sein kann!
Im Internet gibt es zahlreiche Quellen mit Übungsaufgaben, z.B. auf der Lernplattform Serlo.