Überblick
Fragestellung
Gleichungen müssen oftmals nach einer Variablen aufgelöst werden; d.h. man möchte den Wert der Variablen ermitteln, für den die Gleichung wahr ist. Die Lösungsmethoden variieren mit den Gleichungstypen, wobei lineare Gleichungen am einfachsten zu lösen sind (Beispiele anderer Gleichungstypen sind: quadratische, logarithmische, exponentielle, trigonometrische etc. Gleichungen).
In diesem Beitrag geht es um Methoden, wie lineare Gleichungen nach einer Variablen aufgelöst werden können.
Voraussetzungen
- Definition einer linearen Funktion
- Grundgesetze der Arithmetik (Kommutativ-, Assoziativ- und Distributivgesetz)
Kurze Erinnerung:
Eine lineare Funktion y=f(x) ist definiert als: \(y=\color{blue}{m}\cdot x+\color{red}{b}\). Dabei ist m die Steigung und b der Funktionswert bei x=0 (Schnittpunkt mit der y-Achse).
Die Grundgesetze der Arithmetik lauten (a, b, c: reelle Zahlen)
- Kommutativgesetz der Addition bzw. Multiplikation:
\(a+b=b+a\)
\(a\cdot b=b\cdot a\) - Assoziativgesetz der Addition bzw. Multiplikation:
\(\color{blue}{(a+b)}+c=a+\color{blue}{(b+c)}\)
\(\color{blue}{(a\cdot b)}\cdot c=a\cdot \color{blue}{(b\cdot c)}\) - Dissoziativgesetz:
\((a+b)\cdot \color{blue}{c}=a\cdot \color{blue}{c}+b\cdot \color{blue}{c}\)
Außerdem gelten die Grundsätze: „Punkt vor Strichrechnung“ und „Klammern zuerst“.
Was ist eine lineare Gleichung?
Lineare Gleichungen basieren auf der linearen Funktion \(y=m\cdot x+b\). Wichtig ist, dass die Variable x nur in erster Potenz vorkommt und dass sie nicht ihrerseits Argument einer nicht-linearen Funktion ist. Beispiele für nicht-lineare Funktionen:
- \(y=x^2\) (Potenz ungleich 1)
- \(y=sin(x)+3\) (x ist Argument der nicht-linearen Sinus-Funktion)
Dagegen ist \(y=3\cdot (x-1)+4\) eine lineare Funktion, denn die Funktion in der Klammer ist selbst eine lineare Funktion von x. Man kann das sehen, wenn man die Klammer gemäß \(3\cdot (x-1)=3\cdot x-3\) auflöst (Distributivgesetz): \[y=3\cdot x-3+4=3\cdot x+1\]Das ist eine lineare Funktion mit m=3 und b=1.
Achtung: man kann leicht durch das Aussehen einer Gleichung getäuscht werden! Beispiel: \(y=(x-2)\cdot (x+1)\) scheint linear zu sein (jedes x steht in der ersten Potenz). Aber wenn man die Klammern ausmultipliziert, erhält man \(y=x^2-x-2\). Das ist keine lineare, sondern eine quadratische Gleichung!
Schauen wir uns ein Beispiel einer linearen Gleichung an:\[5\cdot x -2=3\cdot x+4\]Es kommen keine nicht-linearen Funktionen vor und alle x stehen in der Potenz eins. Auflösen der Gleichung bedeutet, einen Wert für x zu finden, der die Gleichung wahr macht.
Setzt man beispielsweise 1 für x ein und rechnet die beiden Seiten der Gleichung getrennt aus so ergibt sich:
- linke Seite: \(\color{red}{5\cdot 1}-2=\color{red}{5}-2=3\)
- rechte Seite: \(\color{red}{3\cdot 1}+4=\color{red}{3}+4=7\)
Die beiden Seiten ergeben also für x=1 unterschiedliche Ergebnisse. Die Gleichung ist für x=1 nicht wahr und x=1 ist keine Lösung der Gleichung. Probieren wir x=3:
- linke Seite: \(\color{red}{5\cdot 3}-2=\color{red}{15}-2=13\)
- rechte Seite: \(\color{red}{3\cdot 3}+4=\color{red}{9}+4=13\)
Jetzt ergeben beide Seiten das gleiche Ergebnis; x=3 macht die Gleichung wahr und ist somit eine Lösung.
Soweit, so gut. Allerdings hatten wir die Lösung durch Raten bzw. Ausprobieren erhalten. Die Frage ist, ob es systematische Methoden gibt, eine Lösung zu erhalten (natürlich gibt es die…). Als Erstes werden wir eine geometrische (anschauliche) Lösung besprechen.
Geometrischer Lösungsweg
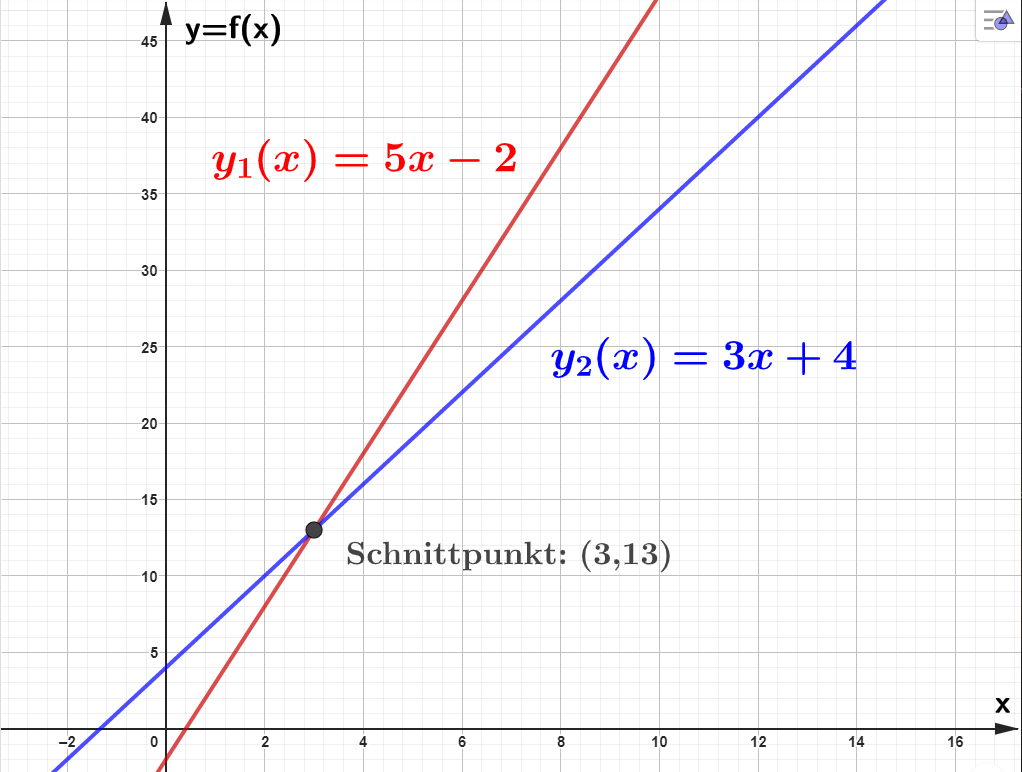
Beide Seiten der Beispielgleichung entsprechen einer linearen Funktion: \(y_1(x)=5x-2\) und \(y_2(x)=3x+4\). Die lineare Gleichung sagt also: wir suchen den x-Wert, bei dem beide Geraden den gleichen y-Wert haben. Mit anderen Worten: wir suchen den Schnittpunkt der beiden Geraden. Abb.1a zeigt den Plot der beiden Geraden samt Schnittpunkt (x=3,y=13).
Die gleiche Situation liegt vor, wenn wir die lineare Gleichung \(5x-2=8\) haben. Denn die rechte Seite entspricht einer Geradengleichung mit m=0 und b=8: \(y=0\cdot m+8=8\). Die beiden Seiten sind bei x=2 gleich, wie man durch Einsetzen prüfen kann: \(5\cdot 2-2=10-2=8\). Der entsprechende Plot ist in Abb.1b zu sehen.
- Nimm die linke Seite der linearen Gleichung als Funktion \(y_1\), die rechte Seite als \(y_2\) und plotte die beiden Funktionen in einem gemeinsamen Graph.
- Bestimme den Schnittpunkt der beiden Gleichungen; seine x-Komponente ist die Lösung der linearen Gleichung.
Noch drei Anmerkungen:
- Es gibt nicht immer eine Lösung! Parallele Geraden haben keinen Schnittpunkt: die Gleichung hat keine Lösung! Das ist immer dann der Fall, wenn die Steigungen \(m_1\) und \(m_2\) der beiden Geraden gleich und die y-Achsenabschnitte \(b_1\) und \(b_2\) verschieden sind. Wir werden dies auch gleich bei der Besprechung der rechnerischen Lösung einer linearen Gleichung sehen.
- Wenn die beiden Seiten die gleiche Gerade beschreiben, gibt es unendlich viele Lösungen. Beispiel: \(5x-3x+4=3+8x-6x+1\). Vereinfacht man die beiden Seiten mit den Grundgesetzen der Arithmetik , so kommt jeweils heraus: \(2x+4\). Die beiden Geraden sind gleich, liegen also übereinander und haben sozusagen unendlich viele Schnittpunkte. Hinweis: die rechnerische Lösung führt auf \(x=x\) und das ist für alle x richtig…
- Wenn die Variable x auf einer Seite der Gleichung mehrfach vorkommt, ist es vorteilhaft, diese Seite so zu vereinfachen, dass x nur noch einmal vorkommt (durch Anwendung der algebraischen Grundgesetze). Dann steht auf beiden Seiten der Gleichung eine einfache Geradengleichung, die wie beschrieben gelöst werden kann.

Do It Yourself !
Klicke auf das Bild und erkunde die grafische Lösung einer linearen Gleichung, indem Du in einem interaktiven Geogebra-Applet Steigung und y-Achsenabschnitt zweier Geraden vorgibst (Bedienungsanleitung unter dem Applet). Anm.: Java muss installiert sein.
Rechnerischer Lösungsweg
Der geometrische Lösungsweg ist zwar sehr anschaulich, hat aber auch Nachteile: Das Plotten der beiden Gleichungsseiten ist zeitintensiv und die Ablesegenauigkeit der Schnittpunktkoordinaten ungenau.
Hier bietet die rechnerische Lösung Vorteile; schauen wir uns an, wie sie funktioniert:
Wenn die Gleichung wahr ist, sind beide Gleichungsseiten gleich (ich weiß: toller Satz…). Verändert man beide Gleichungsseiten auf die gleiche Weise, bleibt die Gleichung wahr. Na gut, etwas weniger abstrakt: Addiert man die gleiche Zahl links und rechts, sind beide Gleichungsseiten nach wie vor wahr. Ebenso, wenn man die Seiten mit der gleichen Zahl multipliziert. Oder beide Seiten quadriert oder, oder, oder.
Das ist die Grundlage jedes algebraischen (rechnerischen) Lösungswegs einer Gleichung (übrigens nicht nur einer linearen Gleichung).
Der „Werdegang“ noch einmal kompakt:
\(5\cdot x -2=3\cdot x+4 \qquad \mid \text{+2}\)
\(5\cdot x=3\cdot x+6 \qquad \mid -3\cdot x\)
\(5\cdot x \ – 3\cdot x = 6 \qquad \mid \text{ links x ausklammern}\)
\((5 – 3)\cdot x = 6 \qquad \mid \text{ Klammer ausrechnen}\)
\(2\cdot x = 6 \qquad \mid \text{ :2}\)
\(x = 3 \qquad \mid \text{ fertig!}\)
Es gibt natürlich noch viele andere Lösungswege: (i) man kann x auf die rechte statt auf die linke Seite bringen; (ii) man kann erst die +4 der rechten Seite durch beidseitige Subtraktion von 4 eliminieren; (iii) man kann beide Seiten durch 5 teilen und dadurch x auf der linken Seite vom Vorfaktor befreien etc. Manche Lösungswege sind einfacher, andere komplizierter (Ansatz (iii) erfordert beispielsweise kompliziertere Rechnungen als die beiden ersten).
Welchen konkreten Lösungsweg man beschreiten sollte, kann man nur durch Übung lernen. Generell sollte man auf beiden Seiten der linearen Gleichung zunächst sämtliche Terme mit x bzw. ohne x zusammenfassen. Dann ist es meist am besten, durch Addition oder Subtraktion die konstanten Summanden auf eine Seite zu bringen und danach dasselbe mit den x-Termen zu tun. Schließlich kann der Vorfaktor im verbleibenden x-Term durch Division entfernt werden. Aber wie gesagt: es kann durchaus vorteilhafte Ausnahmen von diesem Vorgehen geben.
Behandlung der Sondefälle im rechnerischen Lösungsweg
Wir hatten beim geometrischen Lösungsweg gesehen, dass es in einigen Fällen keine (gleiche Steigung, ungleiche y-Achsenabschnitte) oder im Gegenteil unendlich viele (gleiche Steigung, gleiche y-Achsenabschnitte) Lösungen für x geben kann. Wie äußert sich das beim rechnerischen Lösungsweg?
1. Gleiche Steigung, ungleiche y-Achsenabschnitte
Dies entspricht der linearen Gleichung \(m_1 \cdot x + b_1 = m_1 \cdot x + b_2 \). Subtraktion von \(m_1 \cdot x\) auf beiden Seiten führt zu \(b_1 = b_2\). Nach Voraussetzung sind die beiden y-Achsenabschnitte aber verschieden. Die Gleichung kann also niemals wahr sein; es gibt keine Lösung.
2. Gleiche Steigung, gleicher y-Achsenabschnitt
Dies entspricht der linearen Gleichung \(m_1 \cdot x + b_1 = m_1 \cdot x + b_1 \). Subtraktion von \(m_1 \cdot x\) und \(b_1\) auf beiden Seiten führt zu \(0 = 0\), was wahr ist, unabhängig vom x-Wert – oder anders gesagt: sie ist wahr für jeden x-Wert. Es gibt also unendlich viele Lösungen. Die Gleichung ist immer wahr.

Do It Yourself !
Beim Klick auf das Bild kommst Du zu einem interaktiven Geogebra-Applet mit Aufgaben zur Lösung von linearen Gleichungen der Form \(a \cdot x + b = c \cdot x + d \). Die Konstanten a, b, c, und d werden vorgegeben und Du sollst die Gleichung lösen. Anm.: Java muss installiert sein.
für Besserwisser...
Man kann die rechnerische Lösung linearer Gleichungen verallgemeinern und eine Formel zum Auffinden der Lösung entwickeln.
Die Gleichung \(a \cdot x + b = c \cdot x + d\) kann nach x wie üblich aufgelöst werden (\(c \cdot x\) und \(b\) auf beiden Seiten subtrahieren; x ausklammern; durch Vorfaktor dividieren). Man erhält:\[x=\frac{d-b}{a-c}\]Wenn man sich die Formel merkt, kann man die Gleichung also lösen, indem man die Werte für die Konstanten in diese Formel einsetzt und den Bruch ausrechnet (so funktioniert übrigens das Geogebra-Applet).
Die Gleichung \(a \cdot x + b = c \cdot x + d\) ist darüber hinaus ein Spezialfall der Gleichung \[\sum_{i=1}^{n}(a_i \cdot x + b_i)=\sum_{j=1}^{m}(c_j \cdot x + d_j)\]Auftrennen der Summen führt zu\[\sum_{i=1}^{n}a_i \cdot x + \sum_{i=1}^{n}b_i=\sum_{j=1}^{m}c_j \cdot x + \sum_{j=1}^{m}d_j\]Die rechte Summe mit den x-Termen und die linke Summe mit den Konstanten wird durch Subtraktion auf die jeweils andere Seite gebracht:\[\sum_{i=1}^{n}a_i \cdot x – \sum_{j=1}^{m}c_j \cdot x = \sum_{j=1}^{m}d_j -\sum_{i=1}^{n}b_i\]Da x ein gemeinsamer Faktor aller Summanden auf der rechten Seite ist, kann x ausgeklammert werden:\[(\sum_{i=1}^{n}a_i – \sum_{j=1}^{m}c_j )\cdot x = \sum_{j=1}^{m}d_j -\sum_{i=1}^{n}b_i\]Teilen beider Seiten durch die Klammer rechts ergibt die Lösung der allgemeinen linearen Gleichung:\[x=\frac{\sum_{j=1}^{m}d_j -\sum_{i=1}^{n}b_i}{\sum_{i=1}^{n}a_i – \sum_{j=1}^{m}c_j}\]Jede Summe ist insgesamt eine Konstante; die Summen können mit den Konstanten a, b, c und d der einfachen linearen Gleichung identifiziert werden. Jede lineare Gleichung kann also auf die einfache Gleichung zurückgeführt werden!
Drei Sonderfälle können vorkommen:
Zähler=0, Nenner≠0: \(x=0\)
Zähler≠0, Nenner=0: keine Lösung möglich
Man hätte im letzten Schritt die Division gar nicht durchführen dürfen.
Zähler=0, Nenner=0: jedes x ist eine Lösung
Der vorletzte Schritt lautet in diesem Fall \(0\cdot x = 0\), was für alle x richtig ist; die letzte Division ist wieder verboten.
Fazit
- Lineare Gleichungen mit einer Variablen x enthalten diese nur in der ersten Potenz; für die „Besserwisser“: sie haben die allgemeine Form\[\sum_{i=1}^{n}(a_i \cdot x + b_i)=\sum_{j=1}^{m}(c_j \cdot x + d_j)\]
- Jede lineare Gleichung kann auf die Form \(a \cdot x + b = c \cdot x + d \) gebracht werden, deren Lösung für a≠c lautet\[x=\frac{d-b}{a-c}\]
- Ist a=c, gibt es entweder keine Lösung (b≠d) oder unendlich viele (b=d).
- Das Lösen linearer Gleichungen ist ein guter „Trainingsplatz“ für die Anwendung der algebraischen Grundgesetze (Kommutativ- Assoziativ- und Dissoziativgesetz; Punkt-vor-Strichrechnung; Klammern zuerst) und für das Lösen von Gleichungen durch Anwendung gleicher Operationen auf beiden Gleichungsseiten.