Im Beitrag über Natürliche Zahlen und die Grundrechenarten (Addition, Multiplikation, Subtraktion und Division) haben wir die einfachste Zahlenklasse kennengelernt.
Während Addition und Multiplikation von Natürlichen Zahlen generell wieder eine Natürliche Zahl ergeben, ist dies bei Subtraktion und Division nicht immer der Fall. In diesem Beitrag werden wir uns näher mit der Division und den sog. Brüchen beschäftigen, die bei einer Division herauskommen und – etwas „fancy“ – auch Rationale Zahlen genannt werden.
Wo liegt das Problem beim Dividieren ?
Zur Erinnerung: Die Division Natürlicher Zahlen ist nichts anderes als das Aufteilen einer Reihe von Dingen in gleich große Gruppen (jede Teilgruppe bekommt gleich viele Dinge):
- 6 Gummibären können in 3 gleich große Gruppen á 2 Gummibären aufgeteilt werden (6:3 = 2).
- 9 Bananen können zu gleichen Teilen auf 3 Sportler verteilt werden; jeder Sportler bekommt 3 Bananen (9:3 = 3).
- Eine Million Euro können gleichermaßen auf 5 Lottogewinner aufgteilt werden: jeder bekommt 200.000 Euro
1.000.000:5 = 200.000).
Das Ergebnis der Division ist die Anzahl der Dinge in jeder Teilgrupe. Die Division als mathematische Operation ist natürlich unabhängig davon, was aufgeteilt wird: wenn 8 Irgendwas auf 2 Gruppen aufgeteilt werden, bekommt jede Teilgruppe 4 Irgendwas; es gilt immer: 8:2=4.
Bei den gezeigten Beispielen geht die Rechnung – wie man sagt – auf: bei der Aufteilung bleibt nichts übrig. Es gibt aber viele Fälle, in denen ein Rest bleibt: Teilt man 7 Gummibären auf 3 Gruppen auf, bleibt ein Rest von einem Gummibär übrig (7:2=3 Rest 1). Und hier beginnt die Geschichte der rationalen Zahlen.
Abb. 1: 6 Gummibären werden auf 3 Kinder verteilt; es bleibt kein Rest (oben). Verteilt man 7 Gummibären, bleibt dagegen ein Bär als Rest (unten).
Um einen Rest zu vermeiden, muss man den Rest selbst in gleiche Teile aufteilen. Hier bekommen die anschaulichen Beispiele allerdings Probleme. Denn wenn man ein Gummibärchen in 2 Teile spaltet, hat jede Teilgruppe unterschiedliche Elemente (3 ganze und ein halbes Gummibärchen). Wir werden später sehen, wie das zu lösen ist (schon mal ein Hinweis: 3 ganze sind 6 halbe Gummibären…).
Was sind Brüche ?
Die Aufteilung eines Rests schauen wir uns am Beispiel eines Käsekuchens an, der in kleinere Stücke aufgeteilt werden soll (Käsekuchen hat den Vorteil, dass gleich große Stücke gleich aussehen…).
Wenn man den Kuchen in der Mitte durchschneidet, bekommt man 2 gleiche Stücke, die halb so groß sind wie der ganze Kuchen. Man könnte auch sagen: ein Kuchen ist so groß wie zwei halbe Stücke. Man kann den Kuchen auch in 3, 4 oder 6 gleich große Stücke zerschneiden, die dann ein Drittel, ein Viertel oder ein Sechstel genannt werden (der ganze Kuchen besteht dann aus 3 Dritteln, 4 Vierteln oder 6 Sechsteln). Oder allgemein: zerschneidet man den Kuchen in n Stücke (n = 1, 2, 3, …) bekommt man n Stücke der Größe ein n-tel; alle n Stücke zusammen sind wieder so groß wie der ganze Kuchen.
Die Aufteilung in n Stücke entspricht der Division 1:n. Es hat sich für diese Division die Schreibweise \(\frac{1}{n}\) etabliert, die Bruch genannt wird. Der Strich zwischen den Zahlen wird Bruchstrich genannt, die Zahl oberhalb heißt Zähler, die Zahl unterhalb Nenner. Brüche wie \(\frac{1}{4}\) sind kleiner als 1 aber größer als 0; sie sind demnach keine Natürliche Zahl. Brüche stellen eine Erweiterung der Natürlichen Zahlen dar.
Ich möchte betonen, dass der Bruch \(\frac{1}{4}\) nur eine – allerdings sehr nützliche – Schreibweise für das Ergebnis der Division 1 dividiert durch 4 darstellt und damit die Größe eines der Teilstücke angibt (genannt „ein Viertel eines Ganzen“).
Dass in \(\frac{1}{n}\) der Zähler eins beträgt, ist ein Spezialfall eines Bruchs. \(\frac{2}{3}\) (gesprochen „zwei Drittel“) bedeutet, dass es 2 Stücke der Größe ein Drittel gibt. Es ist also dasselbe wie \(\frac{1}{3}+\frac{1}{3}=2\cdot\frac{1}{3}=\frac{2}{3}\).
Und es geht noch allgemeiner: der Zähler kann auch größer als der Nenner sein \(\frac{5}{2}\) bedeutet, dass es sich um 5 Hälften handelt ( \(5\cdot\frac{1}{2}\)). Ist der Zähler kleiner als der Nenner, spricht man von einem echten Bruch. Ist er größer oder gleich dem Nenner, handelt es sich um einen unechten Bruch.
Unecht deshalb, weil man von den 5 Hälften jeweils 2 zu einem Ganzen zusammen fassen kann. Man schreibt dann \(\frac{5}{2}=2\frac{1}{2}\). Wichtig: es gibt in diesem Fall keinen Malpunkt! \(2\frac{1}{2}\) ist eine Abkürzung für \(2+\frac{1}{2}\)! Ein Ausdruck wie \(2\frac{1}{2}\) bzw. \(\frac{5}{2}\) ist ebenfalls eine Rationale Zahl (sie liegt zwischen 2 und 3). Natürliche Zahlen sind eine Teilmenge der Rationalen Zahlen, denn sie können als Brüche mit Nenner 1 aufgefasst werden (\(n=\frac{n}{1}\)).
Erweitern und Kürzen von Brüchen
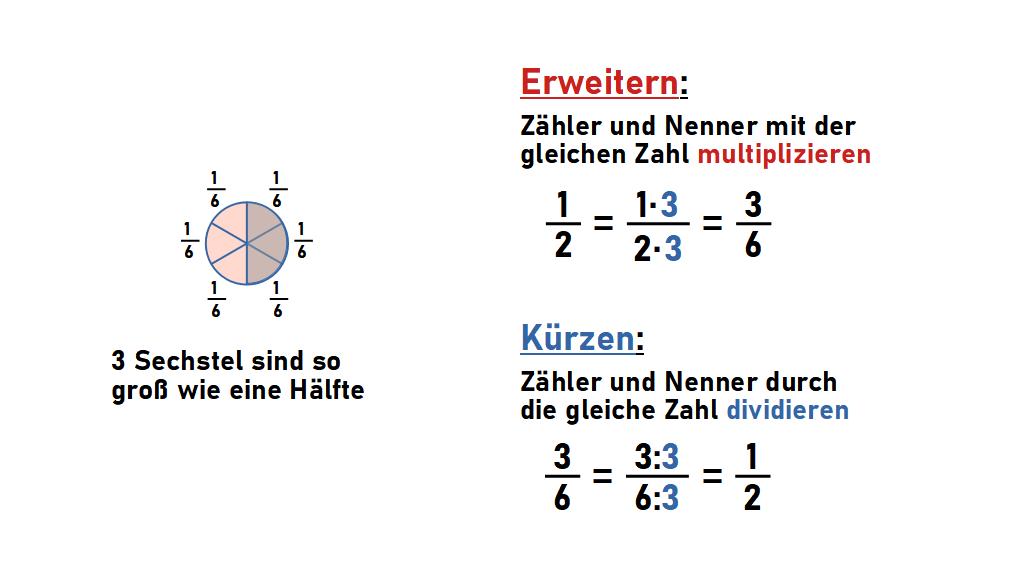
Erweitern und Kürzen ist für das Rechnen mit Brüchen sehr wichtig. Widmen wir uns zunächst dem Erweitern:
Nehmen wir zum Beispiel den Bruch \(\frac{1}{2}\), anschaulich also eine Kuchenhälfte. wenn ich die Kuchenhälfte ihrerseits in 3 gleiche Stücke schneide, bekomme ich 3 Stücke, deren Größe nur noch ein Drittel der Hälfte beträgt. Auf den ganzen Kuchen bezogen sind die einzelnen Stücke nur noch \(\frac{1}{6}\) groß. Es gilt also: \(\frac{1}{2}=3 \cdot\frac{1}{6}=\frac{3}{6}\).
Man kann dies auch allgemeiner formulieren: Wenn man ein Stück der Größe \(\frac{1}{n}\) hat und es in m gleich große Stücke teilt, bekommt man \(m\cdot\frac{1}{n\cdot m}\)Stücke. Dies ist die Essenz des Erweiterns von Brüchen: Wenn man bei einem Bruch Zähler und Nenner mit dem gleichen Faktor multipliziert, bleibt die Größe des Bruchs unverändert.
Statt Zähler und Nenner mit der gleichen Zahl zu multiplizieren, kann man beide auch durch die gleiche Zahl teilen, ohne die Größe des Bruchs zu ändern. Das nennt man dann Kürzen!
Addition von Brüchen
1. Gleicher Nenner
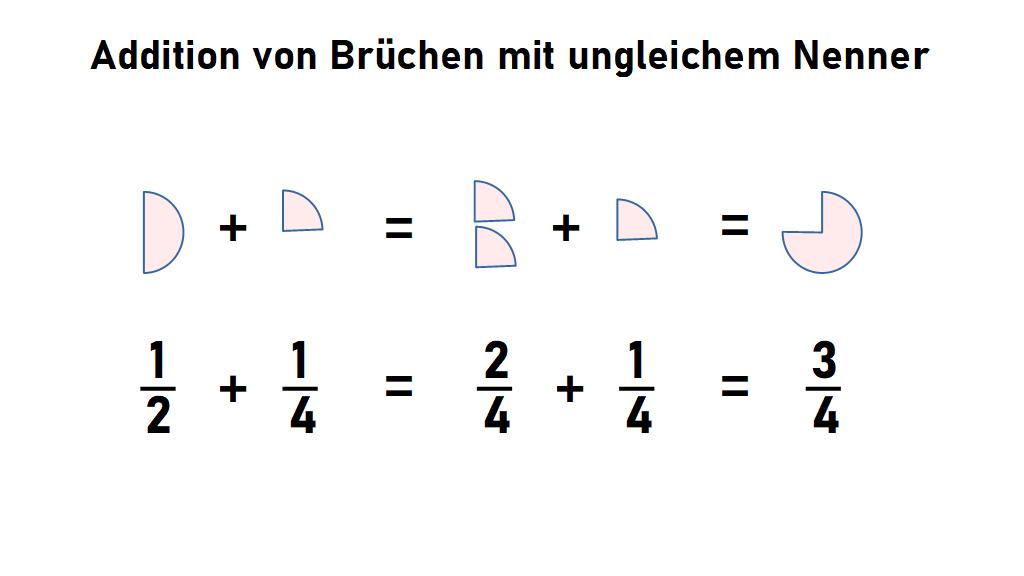
2. Ungleicher Nenner
Bei ungleichem Nenner muss man durch Erweitern oder Kürzen der Brüche die Nenner gleich machen (dadurch wird die Größe des Bruchs nicht verändert!). Danach kann man die Regel für gleiche Nenner anwenden. Ein Beispiel soll das erläutern:
Nehmen wir die Addition einer Hälfte und eines Viertels: \[\frac{1}{2}+\frac{1}{4}\] Die beiden Nenner sind unterschiedlich, sodass sie auf den gleichen Wert gebracht werden müssen. Das kann man erreichen, indem man den ersten Bruch mit dem Faktor 2 erweitert: \[\frac{1}{2}=\frac{2\cdot 1}{2\cdot 2}=\frac{2}{4}\] Jetzt kann die „gleicher Nenner“ Regel angewandt werden: \[\frac{1}{2}+\frac{1}{4}=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}\] Oftmals ist es allerdings nicht so einfach zu sehen, wie man erweitern oder kürzen soll. Es gibt aber einen einfachen Trick, der immer funktioniert: man erweitert den ersten Bruch mit dem Nenner des zweiten und den zweiten Bruch mit dem Nenner des ersten: \[\frac{a}{b}+\frac{c}{d}=\frac{a\cdot d}{b\cdot d}+\frac{c\cdot b}{d\cdot b}\] Im Nenner steht jetzt bei beiden Brüchen b⋅d (bzw. d⋅b, was nach Kommutativgesetz das Gleiche ist), sodass jetzt die beiden erweiterten Zähler addiert werden können: \[\frac{a\cdot d}{b\cdot d}+\frac{c\cdot b}{d\cdot b}=\frac{a\cdot d+c\cdot b}{d\cdot b}\]
Übrigens:
Der Fall gleicher Nenner ist in der allgemeinen Formel für ungleiche Nenner enthalten. Denn für b=d gilt \[\frac{a\cdot b+c\cdot b}{b\cdot b}=\frac{b\cdot(a+c)}{b\cdot b}=\frac{a+c}{b}\]Im ersten Schritt wird das Distributivgesetz angewandt, im zweiten wird duch b gekürzt.
Subtraktion von Brüchen
Die Subtraktion ist schnell abgehandelt: sie funktioniert genauso wie die Addition. Bei gleichem Nenner werden die Zähler subtrahiert und der Nenner beibehalten. Bei ungleichem Nenner müssen die beiden Brüche vor der Subtraktion der Zähler durch Erweitern oder Kürzen auf den gleichen Nenner gebracht werden.
Multiplikation von Brüchen
Brüche zu multiplizieren ist recht einfach. Man multipliziert die beiden Zähler und die beiden Nenner und schon ist man fertig! \[\frac{a}{b}\cdot \frac{c}{d}= \frac{a\cdot c}{b\cdot d}\]Die Begründung ist ein bisschen länglich und verwendet ein paar Kniffe: \(\frac{a}{b}=a\cdot \frac{1}{b}\) und \(\frac{c}{d}=c\cdot \frac{1}{d}\). Das Produkt der beiden Brüche kann man also auch schreiben \[a\cdot \frac{1}{b}\cdot \frac{c}{d}=\frac{1}{b} \cdot a\cdot \frac{c}{d}=\frac{1}{b} \cdot \frac{a \cdot c}{d}\]Jetzt erweitert man den zweiten Bruch mit b und formt wieder um:\[\frac{1}{b} \cdot \frac{a \cdot c}{d}=\frac{1}{b} \cdot \frac{b \cdot a \cdot c}{b \cdot d}=\frac{1}{b} \cdot b \cdot \frac{a \cdot c}{b \cdot d}\]Das war’s schon, denn \[\frac{1}{b} \cdot b=\frac{b}{b}=1\]und der Bruch mit den multiplizierten Zählern und Nennern bleibt übrig.
Anmerkung: eigentlich müsste man noch zeigen, dass das Kommutativgesetz für Brüche gilt. Aus Platzgründen lassen wir das mal weg…
Division von Brüchen
Die Division von Brüchen steht im Ruf, kompliziert zu sein. In Wahrheit ist es aber ganz einfach.
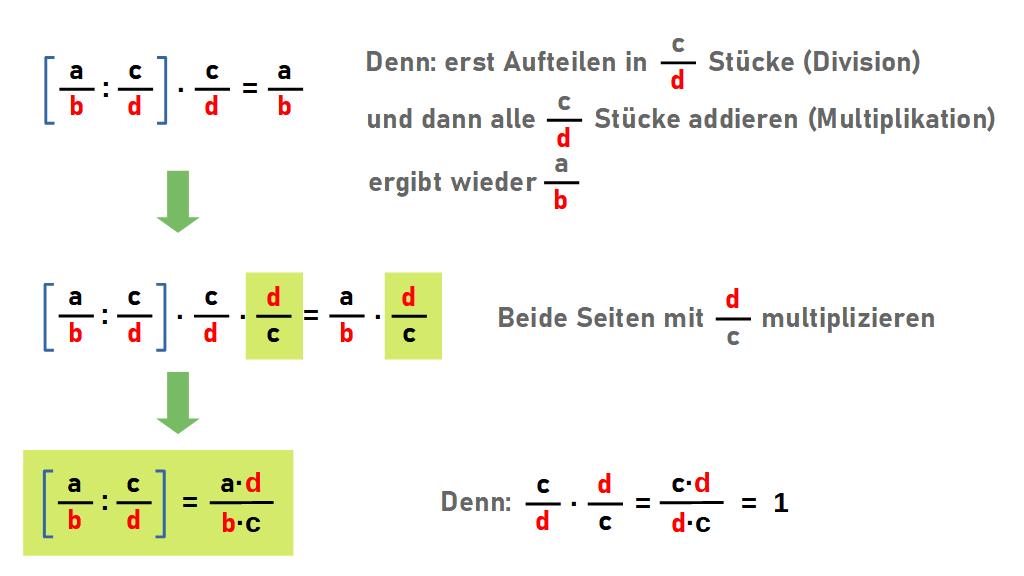
Schreiben wir die Division erst mal ohne Bruch-Schreibweise: \[\frac{a}{b}:\frac{c}{d}\]Laut Definition der Division wird der Bruch \(\frac{a}{b}\) in \(\frac{c}{d}\) Teile geteilt. Wir wissen aus der Division Natürlicher Zahlen, dass Division und Multiplikation mit der gleichen Zahl sich gegenseitig aufheben:\[\frac{a}{n}\cdot n=a\]oder in Worten: Division durch n ist das Gleiche wie Multiplikation mit \(\frac{1}{n}\). Das wenden wir auf die Division der Brüche an:\[\frac{a}{b}:\frac{c}{d}=\frac{a}{b} \cdot \frac{d}{c}=\frac{a \cdot d}{b \cdot c}\]Man kehrt den Bruch \(\frac{c}{d}\) einfach um (der Zähler wird zum Nenner und der Nenner zum Zähler) und multipliziert diesen nach der Multiplikationsregel mit dem Bruch \(\frac{a}{b}\).
Das Ganze kann man auch komplett in Bruch-Schreibweise abhandeln (ich gebe zu: sieht ein wenig merkwürdig aus…):\[\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a \cdot d}{b \cdot c}\]Man dividiert also das Produkt die beiden äußeren Zahlen (a,d) durch das Produkt der beiden inneren Zahlen (b,c).
Zusammenfassung
- Brüche (Rationale Zahlen) sind eine Erweiterung der Natürlichen Zahlen; Natürliche Zahlen werden als Bruch mit Nenner=1 aufgefasst.
- Die Grundrechenarten (Addition, Subtraktion, Multiplikation und Division) sind so definiert, dass sie auch für Natürliche Zahlen gelten.
- Brüche können in verschiedenen Schreibweisen auftauchen (echter Bruch, unechter Bruch mit/ohne ganzzahligem Anteil).
