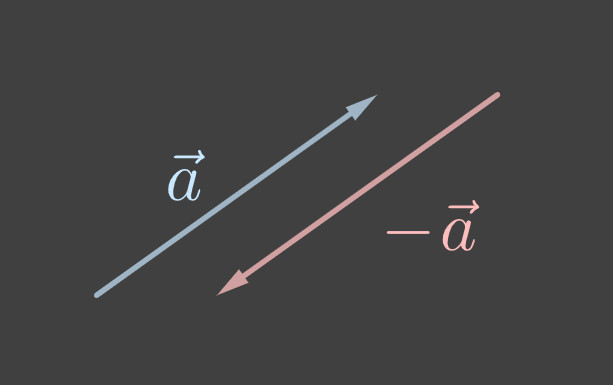Vektoren gehören zu den wichtigsten Objekten in Mathematik und insbesondere Physik. Es gibt physikalische Größen, die durch eine einfache Zahl beschrieben werden. Beispiele sind Temperatur und Masse. Auch in anderen Wissenschaften gibt es solche Größen, z.B. den Geldbetrag einer Ware. Diese Größen werden Skalare genannt.
Speziell in der Physik gibt es aber auch Größen, für die eine Richtung wichtig sind. Die Geschwindigkeit eines Autos ist eine solche Größe: Der Geschwindigkeitsbetrag ist für die Auswirkung eines Aufpralls auf eine Mauer wichtig (je höher die Geschwindigkeit, desto größer der Schaden). Aber auch die Richtung der Geschwindigkeit ist wichtig: Es macht einen großen Unterschied, ob das Auto in Richtung Mauer fährt oder von ihr fort…
Solche richtungsabhängigen Größen können durch Vektoren beschrieben werden.
Also frisch voran (ich weiß: nervig…); schauen wir uns an, was Vektoren sind und wie man mit ihnen rechnet.

Voraussetzungen
Folgende Kenntnisse sind für das Verständnis des Beitrags hilfreich:
- Basiswissen der Trigonometrie (Sinus, Cosinus)
- Kartesische Koordinatensysteme
Geometrische Definition von Vektoren
Um zur geometrischen Definition von Vektoren zu kommen, starten wir mit einem Pfeil. Ein Pfeil ist eine (gerade) Strecke, die in einem Punkt beginnt und einem anderen endet. Er hat eine Länge (Betrag) und eine Richtung und Orientierung (vom Anfangs- zum Endpunkt). Man kann einen Pfeil parallel verschieben (eindimensional entlang seiner Richtung, zweidimensional in einer Ebene oder dreidimensional im Raum), ohne seine Länge, Richtung und Orientierung zu verändern; er bleibt derselbe Pfeil. Oder anders gesagt: sein Anfangspunkt spielt keine Rolle!
Ein Pfeil dessen Anfangspunkt keine Rolle spielt wird Vektor genannt! Oder anders gesagt: ein Vektor ist die Gesamtheit aller Pfeile mit gleicher Länge und Richtung. Vektoren werden of mit einem Pfeil über dem Namen des Vektors bezeichnet: \(\vec{a}\). Sein Betrag, also seine Länge mit \(\mid \vec{a} \mid\).
Da ein konkreter Pfeil einen Vektor repräsentiert, wird im Folgenden immer ein einzelner Pfeil für den entsprechenden Vektor benutzt (es ist schwierig, unendlich viele Pfeile zu zeichnen…). Man kann einen Beispielpfeil eines Vektors parallel verschieben so viel man will (gleiche Länge, gleiche Richtung, unterschiedlicher Anfangspunkt), es bleibt immer derselbe Vektor! Das ist zum Beispiel für die Addition von Vektoren wichtig!
Es drängt sich die Frage auf, warum man zwei Begriffe für parktisch identische Dinge (Pfeil und Vektor) hat. Das liegt daran, dass es andere mathematische Objekte gibt, die sich wie Pfeile verhalten, aber keine sind (Pfeile in höheren Dimensionen, Funktionen als Vektoren, Lösungen von Gleichungssystemen etc.). In diesem Sinne ist ein Pfeil eine spezielle Form eines Vektors.
Besondere Vektoren:
- Ein Vektor, dessen Länge 1 ist, wird als Einheitsvektor oder kürzer als Einsvektor bezeichnet. Es gibt unendlich viele Einheitsvektoren; jeder kann eine andere Richtung haben (Vektoren sind durch Länge und Richtung gekennzeichnet!).
- Ein Vektor mit der Länge 0 heißt verständlicherweise Nullvektor. Ein Nullvektor ist also ein Punkt. Es gibt nur einen Nullvektor, denn er hat keine Richtung (oder, wenn man so will, unendlich viele). Der Nullvektor wird allgemein mit \(\vec{0}\) bezeichnet.
Operationen mit Vektoren
Definition der Addition zweier Vektoren
Zwei Vektoren werden addiert, indem der Anfang des zweiten Vektors an das Ende des ersten gesetzt wird. Die Summe der beiden Vektoren ist der Vektor vom Anfangspunkt des ersten zum Endpunkt des zweiten Vektors. An einem Parallelogramm kann man sich klarmachen, dass die Addition kommutativ ist: die Reihenfolge der Vektoren ist für das Ergebnis der Addition egal (siehe Video 1).
Video 1: Addition zweier Vektoren und Demonstration des Kommutativgesetzes
Definition der Subtraktion zweier Vektoren
Wir beginnen mit der Frage, welchen Vektor \(\vec{x}\) man zu einem gegebenen Vektor \(\vec{a}\) addieren muss, um den Nullvektor zu erhalten – also zum Anfangspunkt zurück zu kommen: \(\vec{a}+\vec{x} = \vec{0}\). Das ist der Vektor, der die gleiche Länge wie \(\vec{a}\) hat, aber in die umgekehrte Richtung zeigt \(\vec{x} = \vec{0} -\vec{a}= -\vec{a}\). Man kann auch sagen: „Anfangs- und Endpunkt werden vertauscht“.
Diese Definition eines negativen Vektors benutzt man zur Subtraktion. So wie man die Subtraktion einer Zahl als Addition der negativen Zahl aufgefasst werden kann, so ist die Subtraktion eines Vektors die Addition seiner negativen Version.
Das Resultat von \(\vec{a}- \vec{b}\) erhält man also, indem \(\vec{b}\) in die Gegenrichtung gedreht und dann zu \(\vec{a}\) addiert wird; der Differenzvektor reicht dann vom Anfangspunkt von \(\vec{a}\) zum Endpunkt von \(-\vec{b}\).
Definition der Multiplikation eines Vektors mit einer Zahl
Zunächst mal: Vektoren und Zahlen sind zwei offensichtlich verschiedene Dinge. Die Multiplikation einer Zahl mit einem Vektor muss also eigens definiert werden. Das kann in sinnvoller Weise geschehen, indem man so weit wie möglich die Definition der Multiplikation von Zahlen auf Vektoren überträgt.
Bei Zahlen ist Multiplikation die mehrfache Addition der gleichen Zahl\[3 \cdot 5 = 5 + 5 + 5\]Ganz analog kann man definieren: die Multiplikation einer Zahl mit einem Vektor ist die mehrfache Addition des Vektors zu sich selbst:
Man muss den Vektor einfach dreimal aneinander fügen. Das Ergebnis der Multiplikation ist ein Vektor mit der gleichen Richtung aber der dreifachen Länge. Oder allgemein: \(m \cdot \vec{a}\) (m: reelle Zahl; \(\vec{a}\): Vektor) ist das Gleiche wie m Vektoren \(\vec{a}\) nacheinander zu addieren. Der Ergebnisvektor hat die m-fache Länge und die gleiche Richtung wie \(\vec{a}\).
Ist m>1, wird der Vektor länger, ist m<1 wird er kürzer. Multiplikation mit 1 lässt den Vektor unverändert, Multiplikation mit 0 ergibt den Nullvektor.
Wenn ein Vektor mit einer negativen Zahl multipliziert wird, dreht er seine Richtung um (siehe oben: \(-\vec{a}\) ist der Vektor \(\vec{a}\) mit umgekehrter Richtung).
Multiplikation zweier Vektoren (Skalarprodukt)
Jetzt wird es komplizerter. Addition zweier Vektoren und Multiplikation eines Vektors mit einer Zahl waren sehr ähnlich zur Addition und Multiplikation von Zahlen. Die Multiplikation zweier Vektoren ist aber etwas ganz anderes.
Hat man zwei Vektoren, ist es oft von Interesse, „vielviel der Länge“ eines Vektors in Richtung des anderen Vektors zeigt. Dies war in der Physik eine wichtige Fragestellung, weil Kraft als Vektor aufgefasst werden kann und man den Anteil der Kraft in einer vorgegebenen Richtung ermitteln wollte, die nicht die Richtung der Kraft war.
Werden wir etwas konkreter: Wir haben zwei Vektoren \(\vec{a}\) und \(\vec{b}\), die einen Winkel φ (griechischer Buchstabe „phi“) zueinander einnehmen. Lässt man beide Vektoren von einem gemeinsamen Anfangspunkt ausgehen, sieht man, dass \(\vec{a}\) die Summe aus zwei Vektoren ist, von denen einer (\(\vec{a}_{||}\)) parallel zu \(\vec{b}\) und einer senkrecht dazu ist (\(\vec{a}_{\perp}\)). Die Länge des parallelen Vektors erhält man aus dem Cosinus von φ, da \(\vec{a}\), \(\vec{a}_{||}\)und \(\vec{a}_{\perp}\) ein rechtwinkliges Dreieck bilden (siehe Video 3).
Dann ist die Länge von \(\vec{a}_{||}\) gleich der Länge von \(\vec{a}\) multipliziert mit dem Cosinus von φ (zur Erinnerung: Cosinus = Gegenkathete durch Hypotenuse)\[a_{||}=\mid \vec{a} \mid \cdot \cos{\varphi}\]
Video 3: Skalarprodukt zweier Vektoren
Da man in den physikalischen Anwendungen meist an dem Produkt aus dem Betrag von \(\vec{a}_{||}\) und dem Betrag von \(\vec{b}\) interessiert ist, hat man dieses Produkt Skalarprodukt zweier Vektoren genannt: \[\vec{a}\cdot \vec{b}=a_{||}\cdot \mid \vec{b} \mid = \mid \vec{a} \mid \cdot \mid \vec{b} \mid \cdot \cos(\varphi)\]Das Skalarprodukt ist also eine Zahl, kein Vektor!
Man sagt auch, das Skalarprodukt ist das Produkt aus der Länge der Projektion von \(\vec{a}\) auf die Richtung von \(\vec{b}\) und der Länge von \(\vec{b}\). Übrigens: das Skalarprodukt ist kommutativ: \(\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a}\). Denn \(\mid \vec{b} \mid \cdot \cos{\varphi}\) ist die Länge der Projektion von \(\vec{b}\) auf die Richtung von \(\vec{a}\).
Sonderfälle:
- Stehen die beiden Vektoren senkrecht aufeinander, ist das Skalarprodukt 0, denn \(\cos{90°}=0\)
- Sind die beiden Vektoren parallel zueinander, ist das Skalarprodukt gleich dem Betragsprodukt der beiden Vektorbeträge, denn \(\cos{0°}=1\).
- Das Skalarprodukt eines Vektors mit sich selbst entspricht dem Quadrat seiner Länge: \(\vec{a}\cdot\vec{a}=\mid \vec{a} \mid \cdot \mid \vec{a} \mid \cdot \cos{0°}={\mid \vec{a} \mid}^2\), denn \(\cos{0°}=1\).
- Das Skalarprodukt eines Vektors mit seiner (gleich langen) antiparallelen Version entspricht seinem negativen Längenquadrat, da \(\cos{180°}=-1\)!
- Ist der Vektor \(\vec{b}\) ein Einheitsvektor (Betrag = 1), ist das Skalarprodukt gleich der Länge von \(\vec{a}_{||}\); Gleiches gilt umgekehrt, wenn \(\vec{a}\) ein Einheitsvektor ist.
- Das Skalarprodukt ist negativ, wenn der Winkel zwischen 90° und 270° beträgt, denn der Cosinus ist in diesem Wertebereich von φ negativ. Bei Winkeln zwischen 0° und 90° bzw. zwischen 270° und 360° ist das Skalarprodukt positiv.
Anmerkung zwei:
Es gibt noch ein weiteres Produkt zweier Vektoren, das sog. Vektorprodukt, das ebenfalls in der Physik eine Rolle spielt. An dieser Stelle wollen wir aber darauf nicht näher eingehen. Nur soviel: Das Vektorprodukt zweier Vektoren \(\vec{a}\) und \(\vec{b}\) ist wieder ein Vektor (im Gegensatz zum Skalarprodukt), der senkrecht auf den beiden Vektoren steht und dessen Länge \(\mid \vec{a} \mid \cdot \mid \vec{b} \mid \cdot \sin{\varphi}\) beträgt.
Vektoren in Koordinatensystemen
Wir haben gesehen, wie Vektoren geometrisch definiert sind und die wichtigsten Rechenoperationen kennengelernt. Die Rechenoperationen haben allerdings den Nachteil, dass das Rechnen nur mit „Bleistift und Lineal“ möglich ist. Es wäre aber sehr wünschenswert, auch algebraisch – also mit Zahlen – mit Vektoren umgehen und rechnen zu können.
Das ist möglich, wenn wir Vektoren in Koordinatensystemen betrachten. Wir werden uns jetzt diesem wichtigen Thema zuwenden, wobei wir uns auf kartesische Koordinatensysteme beschränken. In der Praxis wird fast ausschließlich mit dieser Methode gerechnet und in vielen Lehrbüchern werden Vektoren sogar mit Hilfe von Koordinatensystemen eingeführt.
In einem anderen Beitrag haben wir bereits gezeigt, was Koordinatensysteme sind und wofür sie gebraucht werden. Dort war allerdings von Vektoren noch keine Rede; das holen wir jetzt nach…
Zur Erinnerung:
- Ein kartesisches Koordinatensystem (Abb.2) besteht aus zwei oder drei senkrecht aufeinander stehenden und sich in einem Punkt schneidenden Achsen, die gewöhnlich x-, y- und z-Achse genannt werden (zwei Achsen in der 2-dim. Ebene und drei im 3-dim. Raum).
- Der gemeinsame Schnittpunkt der Achsen wird Koordinatenursprung (oder kurz: Ursprung) genannt.
- Jede Achse ist ein Zahlenstrahl, auf dem eine Einheitslänge definiert ist.
- Dadurch kann die Position eines Punktes in der Ebene oder im Raum eindeutig durch drei Zahlen gekennzeichnet werden, die die (senkrechte) Entfernung des Punktes zu den zwei oder drei Achsen angeben.

Man kann die Lage eines Punkts im Koordinatensystem durch seinen Abstand von der x- und y-Achse angeben. Aber es ist auch möglich, mit den Koordinaten des Punktes einen Vektor zu beschreiben, der vom Ursprung zum Punkt reicht. Einen solchen Vektor, dessen Anfang an einem festgelegten Ort liegt, wird Ortsvektor genannt. Es ist in gewisser Weise der spezielle Pfeil des Vektors, der vom Ursprung ausgeht (Video 4).
Dadurch muss man zur Festlegung eines Vektors nur noch den Endpunkt angeben; denn der Anfangspunkt ist vereinbarungsgemäß immer (0/0). Anm.: immer dran denken: ein spezieller Pfeil ist ein Repräsentant des Vektors, zu dem er gehört!
Der Witz am Gebrauch eines Koordinatensystems ist, dass man damit jeden Vektor (bzw. jeden Pfeil als seinen Repräsentanten) durch die Koordinaten seines Anfangs- und Endpunktes eindeutig charakterisieren kann! Bei Ortsvektoren ist der Anfangspunkt für alle Vektoren derselbe: der Koordinatenursprung.
Video 4: Ortsvektoren
Vektoren als Linearkombination von Einheitsvektoren
Im Folgenden werden wir der Einfachheit halber von Vektoren in einer Ebene ausgehen (das lässt sich leichter zeichnen). Die Ergebnisse können aber auf Vektoren im Raum übertragen werden.
In der Ebene braucht man zur eindeutigen Charakterisierung eines Ortsvektors zwei Zahlen: die x- und die y-Komponente. Äquivalent dazu ist die Charakterisierung des Ortsvektors durch eine Linearkombination von Einheitsvektoren möglich. Hört sich schlimm an, ist aber ziemlich einfach – und in der Praxis von grundlegender Bedeutung für das Rechnen mit Vektoren.
Alle Vektoren in Richtung der x-Achse können als Vielfache des Einheitsvektors auf der x-Achse beschrieben werden: \(\vec{a_x}= m \cdot \vec{e_x}\) mit \(m \in{\mathbb{R}}\). Ebenso können alle Vektoren in Richtung der y-Achse als Vielfaches des Einheitsvektors auf der y-Achse aufgefasst werden: \(\vec{a_y}= m \cdot \vec{e_y}\).
Und jeder Vektor \(\vec{a}\) ist die Summe der beiden Vektoren \(\vec{a_x}\) und \(\vec{a_y}\) (Abb.3). Im Beispiel ist
\(\vec{a_x}=5\cdot \vec{e_x}\),
\(\vec{a_y}=4\cdot \vec{e_y}\) und
\(\vec{a}=5\cdot \vec{e_x}+4\cdot \vec{e_y}\)
An dieser Stelle bewahrheitet sich mal wieder der Spruch: „Mathematik ist der Versuch, Faulheit zum Prinzip zu erheben“. Denn man möchte sich Schreibarbeit sparen. Statt\[\vec{a}=5\cdot \vec{e_x}+4\cdot \vec{e_y}\]schreibt man kürzer\[\vec{a}=\begin{pmatrix} 5 \\ 4 \end{pmatrix}\]oder allgemeiner: statt\[\vec{a}=x\cdot \vec{e_x}+y\cdot \vec{e_y}\]schreibt man\[\vec{a}=\begin{pmatrix} x \\ y \end{pmatrix}\]Die Einheitsvektoren in x- und y-Richtung werden auch Basisvektoren genannt, da man mit ihnen alle Vektoren der Ebene durch Linearkombination darstellen kann. Und die Zahlen x und y werden Komponenten von \(\vec{a}\) in der Basis \(\vec{e_x}\)/\(\vec{e_y}\) genannt. In Komponentenschreibweise lauten die Einheitsvektoren\[\vec{e_x}=\begin{pmatrix} 1 \\ 0 \end{pmatrix}\qquad \vec{e_y}=\begin{pmatrix} 0 \\ 1 \end{pmatrix} \]
Will man Vektoren im 3-dim. Raum auf diese Weise beschreiben, braucht man noch einen dritten Einheitsvektor in Richtung der z-Achse. Ein Vektor ist dann die Linearkombination \(\vec{a}=x\cdot \vec{e_x}+y\cdot \vec{e_y}+z\cdot \vec{e_z}\) bzw. \(\vec{a}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}\). Die Einheitsvektoren lauten dann\[\vec{e_x}=\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\qquad \vec{e_y}=\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\qquad \vec{e_z}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\qquad\]
Im Folgenden werden wir uns anschauen, wie die Rechenoperationen, die wir im geometrischen Bild kennengelernt haben, in der Koordinatendarstellung funktionieren.
Algebaische Addition von Vektoren
Um Zeit und Schreibarbeit zu sparen, wird es jetzt ein wenig spartanisch bzw. formellastig. Wir nehmen zwei Vektoren \(\vec{a}\) und \(\vec{b}\). Die beiden lassen sich als Linearkombination der Basisvektoren \(\vec{e_x}\) und \(\vec{e_y}\) darstellen:
\(\vec{a}=a_x\cdot \vec{e_x}+a_y\cdot \vec{e_y}\)
\(\vec{b}=b_x\cdot \vec{e_x}+b_y\cdot \vec{e_y}\).
Bei der Addition der beiden erhält man:\[\vec{a}+\vec{b}=a_x\cdot \vec{e_x}+a_y\cdot \vec{e_y}+b_x\cdot \vec{e_x}+b_y\cdot \vec{e_y}\]Umordnung und Ausklammern der Basisvektoren führt zu\[\vec{a}+\vec{b}=(a_x+b_x)\cdot \vec{e_x}+(a_y+b_y)\cdot \vec{e_y}\]Man addiert also zwei Vektoren, indem man die Komponenten ihrer Basisvektoren addiert. In Komponentenschreibweise:\[\vec{a}+\vec{b}=\begin{pmatrix} a_x \\ a_y \end{pmatrix}+\begin{pmatrix} b_x \\ b_y \end{pmatrix}=\begin{pmatrix} a_x+b_x \\ a_y+b_y \end{pmatrix}\]
Algebraische Subtraktion von Vektoren
Bei der Subtraktion der Vektoren \(\vec{a}\) und \(\vec{b}\) erhält man:\[\vec{a}-\vec{b}=a_x\cdot \vec{e_x}+a_y\cdot \vec{e_y}-b_x\cdot \vec{e_x}- b_y\cdot \vec{e_y}\]Umordnung und Ausklammern der Basisvektoren führt zu\[\vec{a}-\vec{b}=(a_x-b_x)\cdot \vec{e_x}+(a_y-b_y)\cdot \vec{e_y}\]Man subtrahiert also zwei Vektoren, indem man die Komponenten ihrer Basisvektoren subtrahiert. In Komponentenschreibweise:\[\vec{a}-\vec{b}=\begin{pmatrix} a_x \\ a_y \end{pmatrix}-\begin{pmatrix} b_x \\ b_y \end{pmatrix}=\begin{pmatrix} a_x-b_x \\ a_y-b_y \end{pmatrix}\]
Algebraische Multiplikation eines Vektors mit einer Zahl
Die Multiplikation eines Vektors \(\vec{a}\) mit einer Zahl \(m\) nutzt die Geltung des Distributivgesetzes aus:\[m\cdot \vec{a}=m\cdot (a_x \vec{e_x}+a_y \vec{e_y})=m\cdot a_x \vec{e_x}+m\cdot a_y \vec{e_y}\]Oder in Komponentendarstellung:\[m\cdot \begin{pmatrix} a_x \\ a_y \end{pmatrix}=\begin{pmatrix} m\cdot a_x \\ m\cdot a_y \end{pmatrix}\]Man multipliziert also einfach die Komponenten mit \(m\).
Algebraische skalare Multiplikation zweier Vektoren
Wieder geht man von der Darstellung der beiden Vektoren als Linearkombination von Einheitsvektoren aus. Dann gilt:\[\vec{a}\cdot\vec{b}=(a_x \vec{e_x}+a_y \vec{e_y})\cdot (b_x \vec{e_x}+b_y \vec{e_y})\]Ausmultiplizieren der Klammer führt zu
\[a_x\cdot b_x\cdot \color{red}{\vec{e_x}\cdot \vec{e_x}}+a_x\cdot b_y\cdot \color{blue}{\vec{e_x}\cdot \vec{e_y}}+\\a_y\cdot b_x\cdot \color{blue}{\vec{e_y}\cdot \vec{e_x}}+a_y\cdot b_y\cdot \color{red}{\vec{e_y}\cdot \vec{e_y}}\]
\(\vec{e_x}\) und \(\vec{e_y}\) stehen im kartesischen Koordinatensystem aber senkrecht aufeinander (Winkel: 90°), sodass die beiden gemischten Produkte der Einheitsvektoren Null (blau markiert) ergeben. Ein Einheitsvektor mit sich selbst multipliziert (rot markiert) ergibt eins. Setzt man die Produkte der Einheitsvektoren ein, landet man bei\[\vec{a}\cdot\vec{b}=a_x\cdot b_x+a_y\cdot b_y\]
Man bekommt also zwei Darstellungen des Skalarprodukts: aus der geometrischen Definition \(\mid \vec{a} \mid \cdot \mid \vec{b} \mid \cdot \cos(\varphi)\) und aus der Darstellung mit Basisvektoren \(a_x\cdot b_x+a_y\cdot b_y\). Setzt man die beiden gleich und dividiert durch die Beträge der beiden Vektoren (beides sind Zahlen) erhält man einen Ausdruck für cos(φ):\[\cos{\varphi}=\frac{a_x\cdot b_x+a_y\cdot b_y}{\mid \vec{a} \mid \cdot \mid \vec{b} \mid}=\frac{\vec{a}\cdot \vec{b}}{\mid \vec{a} \mid \cdot \mid \vec{b} \mid}\]
Ausblick
In diesem einführenden Beitrag konnte nur ein erster Einblick in die Welt der Vektoren und ihrer Anwendungen gegeben werden. Beispiele für Anwendungen sind:
- Zahlen werden auf der Zahlengeraden als Pfeile dargestellt, also als eindimensionale Vektoren, für die man nur eine Komponente braucht.
- Der Vektorbegriff kann auch in höheren Dimensionen verwendet werden; man muss nur die Anzahl der Koordinatenachsen bzw. der Vektorkomponenten erhöhen (allerdings kann das nicht mehr zeichnerisch dargestellt werden, da wir uns nur die drei Dimensionen unseres normalen Raums vorstellen können). So wird die Mathematik der speziellen Relativitätstheorie durch die Verwendung von Vektoren mit 4 Komponenten (sog. 4er-Vektoren) besonders einfach.
- Man kann auch vom anschaulichen Vektorbegriff komplett abstrahieren, indem man mathematische Objekte und Rechenoperationen definiert, die sich so wie geometrische Vektoren verhalten. Dies wird in vielfältiger Weise in der Quantenmechanik angewandt.
- Lineare Gleichungssysteme, die in der Statistik, bei Optimierungsproblemen und vielen anderen Anwendungen wichtig sind, können besonders elegant mit Hilfe von Vektoren und sog. Matrizen (einer Erweiterung des Vektorbegriffs) gelöst werden.
- Computerspiele oder bildgebende Verfahren in der Medizin müssen eine 3-dimensionale Welt auf einen Bildschirm projizieren – und das aus verschiedenen Blickwinkeln. Vektoren spielen als mathematische Hilfsmittel auch hier eine zentrale Rolle.
Fazit
- Ein Vektor ist die Gesamtheit aller Pfeile mit gleicher Länge (Betrag) und Richtung.
- Vektoren können geometrisch oder als Linearkombination von Einheitsvektoren (Basisvektoren) in einem kartesischen Koordinatensystem dargestellt werden. Letzteres erlaubt ein algebraisches Rechnen mit Vektoren. Die Koeffizienten der Einheitsvektoren werden Komponenten bezüglich einer Basis genannt.
- Addition von Vektoren
- geometrisch: Vektoren \(\vec{a}\) und \(\vec{b}\) werden addiert, indem der Anfangspunkt von \(\vec{b}\) an den Endpunkt von \(\vec{a}\) gesetzt wird; der Summenvektor reicht vom Anfangspunkt von \(\vec{a}\) zum Endpunkt von \(\vec{b}\).
- algebraisch: Man addiert zwei Vektoren, indem ihre Komponenten addiert werden.
- Subtraktion von Vektoren
- geometrisch: Vektor \(\vec{b}\) wird von Vektor \(\vec{a}\) subtrahiert, indem die Richtung von \(\vec{b}\) umgekehrt wird und der umgekehrte Vektor zu \(\vec{a}\) addiert wird.
- algebraisch: Die Komponenten von \(\vec{b}\) werden von den Komponenten von \(\vec{a}\) subtrahiert.
- Multiplikation eines Vektors mit einer Zahl
- geometrisch: \(m\cdot \vec{a}\) bedeutet, dass m Vektoren \(\vec{a}\) addiert werden.
- algebraisch: Alle Komponenten von \(\vec{a}\) werden mit m multipliziert.
- Das Skalarprodukt zweier Vektoren ist eine Zahl!
- geometrisch: die Länge der Projektion von \(\vec{a}\) in Richtung von \(\vec{b}\) wird mit der Länge von \(\vec{b}\) multipliziert: \(\vec{a}\cdot \vec{b}=\mid\vec{a}\mid \cdot \mid\vec{b}\mid \cdot \cos{\varphi}\)
- algebraisch: die zugehörigen Komponenten von \(\vec{a}\) und \(\vec{b}\) werden multipliziert und die Produkte addiert: \(\vec{a}\cdot\vec{b}=a_x\cdot b_x+a_y\cdot b_y\)
- Wenn \(\vec{a}\) senkrecht auf \(\vec{b}\) ist das Skalarprodukt 0
- Wenn \(\vec{a}\) parallel zu \(\vec{b}\) ist das Skalarprodukt gleich dem Produkt der Vektorbeträge.
- Das Skalarprodukt von kartesischen Einheitsvektoren mit sich selbst ist 1; gemischte Produkte von kartesischen Einheitsvektoren haben den Wert 0.