Trigonometrische Funktionen (Sinus, Cosinus, Tangens etc.) spielen in vielen Bereichen der angewandten Wissenschaften – insbesondere in der Physik – eine sehr wichtige Rolle. So werden Schwingungen und Wellen durch trigonometrische Funktionen beschrieben. Und diese wiederum sind für alle Physikalischen Teilgebiete extrem wichtig: Mechanik, Elektrodynamik, Quantenmechanik („Wellenmechanik“) etc.
Deshalb schauen wir uns in folgenden Beitrag die Eigenschaften trigonometrischer Funktionen näher an.
Was sind trigonometrische Funktionen?
Ursprünglich wurden die Sinus- und Cosinusfunktion am rechtwinkligen Dreieck definiert (daher die Bezeichnung „trigonometrisch“ vom griechischen Wort trigonon für Dreieck).
Wenn in einem Dreieck ein Winkel 90° beträgt, spricht man von einem rechtwinkligen Dreieck (Abb.1). Die dem rechten Winkel (der Winkel mit dem Punkt, oben in der Graphik) gegenüber liegende Dreiecksseite heißt Hypotenuse. Ebenfalls eingezeichnet ist der Winkel φ. Die an ihm anliegende Seite heißt seine Ankathete, die ihm gegenüber liegende seine Gegenkathete.
Der Sinus des Winkels φ – sin(φ) – ist das Längenverhältnis seiner Gegenkathete zur Hypotenusenlänge, der Cosinus – cos(φ) – ist das entsprechende Längenverhältnis der Ankathete zur Hypotenuse.

Übrigens:
Winkel können auf zweierlei Art angegeben werden: in Grad oder als Bogenmaß.
Die Gradeinteilung ist den meisten geläufig: der rechte Winkel beträgt 90°, der Winkel des Halbkreises 180° und der Winkel des Vollkreises 360°. Daran hat man sich gewöhnt. Für viele Anwendungen ist es aber wesentlich besser, das Bogenmaß zu benutzen, dessen Einheit rad (von radian) genannt wird.
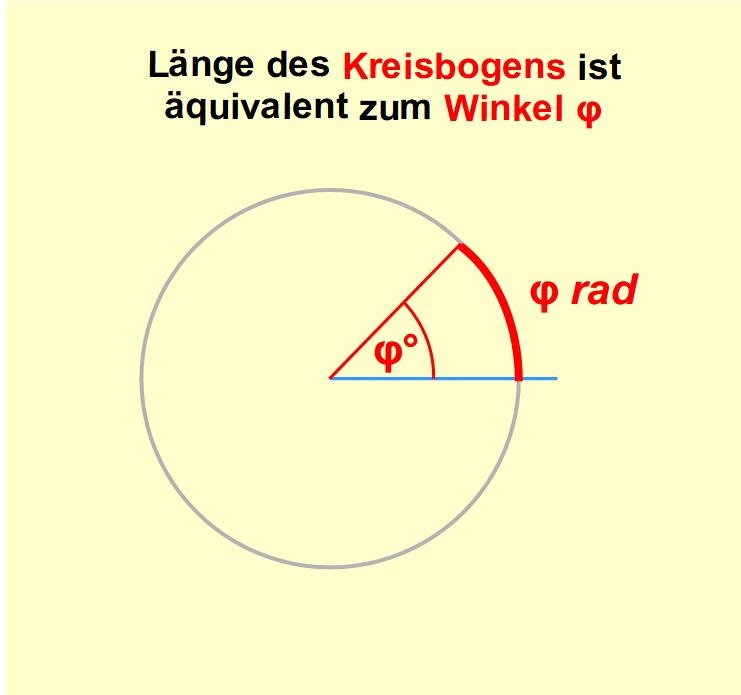
Das Bogenmaß beruht darauf, dass ein Kreis mit Radius 1 einen Umfang von 2π hat (denn: Umfang eines Kreises mit Radius r ist gleich 2πr). Ein Winkel von 360° ist also äquivalent zur Länge eines Kreisbogens von 2π (in der gleichen Weise sind 60 Sekunden äquivalent zu 1 Minute). Ist der Kreisbogen nur halb so groß (π) halbiert sich auch der Winkel (180°). Es handelt sich also um eine Umrechnung in eine andere Winkeleinheit. Diese wird rad genannt.
Da die Kreisbogenlänge proportional zu ihrem Winkel ist, gilt:\[\frac{2\pi}{360}=\frac{\varphi(\text{rad})}{\varphi(\text{grad})}\]Die Umrechnung von Grad in rad lautet also:\[\varphi(\text{rad})=\frac{2π}{360}\varphi(\text{grad})\]Ein rad entspricht also 360/2π≈57,3°.
Schauen wir uns an, wie die Funktionskurven von sin(φ) und cos(φ) zustande kommen. Dazu bedient man sich eines Tricks: Man betrachtet in einem Koordinatensystem ein rechtwinkliges Dreieck in einem Kreis mit dem Radius R (Abb. 2). Mit dem beschriebenen Verfahren erreicht man auch, dass die trigonometrischen Funktionen für Winkel größer als 90° (π/2 rad) definiert sind, obwohl das im rechtwinkligen Dreieck nicht möglich ist.
Der Punkt P liegt auf dem Kreisradius; seine Entfernung von der x-Achse beträgt y. Der Koordinatenursprung (0/0), P (x,y) und der Punkt (x/0) auf der x-Achse bilden ein rechtwinkliges Dreieck. y ist die Gegenkathete des Winkels φ. Dann ist y/R geich dem Sinus von φ! Wenn R=1 gewählt wird ist die Länge von y gleich sin(φ)!
Trägt man die Länge von y für verschiedene φ-Werte in ein Koordinatensystem mit den φ-Werten auf der x-Achse ein, hat man die Funktionskurve von sin(φ) vor sich. Dies ist in der untenstehenden Animation demonstriert.
Trägt man statt der y-Werte die x-Werte gegen den Winkel φ auf, so erhält man die Funktionskurve der Cosinusfunktion cos(φ). Denn in Abb.2 ist x die Ankathete des Winkels φ.
In Abb. 3 sind Sinus und Cosinus in einem Graph zusammen dargestellt. sin(φ) schneidet die y-Achse im Ursprung, cos(φ) bei 1. Außerdem sieht man, dass die beiden Funktionskurven die gleiche Form haben. sin(φ) ist allerdings um den Winkel π/2 (90°) gegen cos(φ) nach rechts verschoben.
Zwischenfazit:
- Der Funktionsverlauf wiederholt sich, wenn der Winkel um 2π≈6,28… vergrößert wird; am besten zu sehen an der Lage der Maxima und Minima. sin(φ) und cos(φ) sind periodische Funktionen.
- Für φ=0 ist die Länge der Gegenkathete null: \(\sin(0)=0\).
- Für φ=0 ist die Länge der Ankathete eins: \(\cos(0)=1\).
- Sinus- und Cosinus-Funktion haben die gleiche Gestalt, sind aber um den Winkel π/2 gegeneinander verschoben.
Modifikationen von Sinus und Cosinus
Bisher haben wir uns nur mit den einfachsten Formen einer Sinus- und Cosinusfunktion beschäftigt. Schauen wir uns an, welche Modifikationen man machen kann.
Multiplikation mit einer Zahl
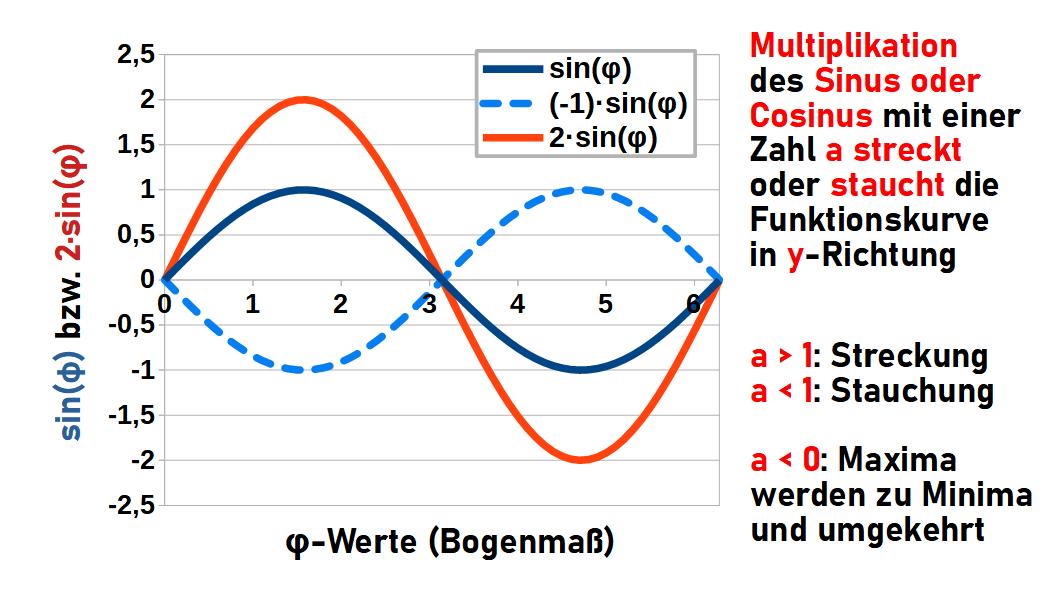
Durch Multiplikation mit der Zahl a wird aus \(y_1=\sin{(x)}\) die Funktion \(y_2=a \cdot \sin{(x)}\). Jeder y-Wert wird gegenüber sin(φ) a-mal größer. Anschaulich gesprochen: der Ausschlag nach oben und unten wird um den Faktor a vergrößert. Die Höhe des Ausschlags wird Amplitude genannt und ist eine wichtige Größe zur Charakterisierung einer Sinus- oder Cosinusfunktion. Die Differenz zwischen Maximum und Minimum entspricht der doppelten Amplitude.
Eine Animation verdeutlicht den Einfluss der Amplitude auf die Kurvenform.
Ist a > 1 wird die Funktionskurve von sin(φ) in y-Richtung gestreckt, ist a < 1 wird sie gestaucht (solange a > 0). Ist a negativ, wird nicht nur gestreckt/gestaucht, sondern die Funktionskurve wird zusätzlich an der x-Achse gespiegelt; Maxima werden zu Minima und umgekehrt.
Addition einer Zahl
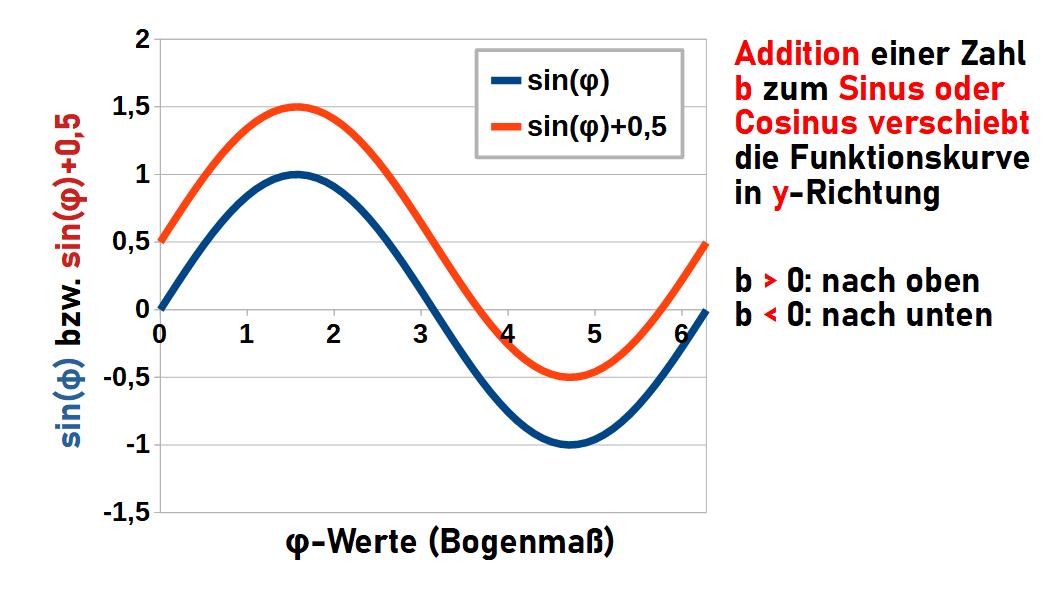
Ganz anders wirkt sich die Addition einer Zahl b zum Sinus oder Cosinus aus. In diesem Fall kommt es nicht zur Streckung/Stauchung der Funktionskurve, sondern zu einer Verschiebung der kompletten Kurve in y-Richtung, ohne dass sich die Form der Kurve ändert.
Ist b > 0, wandert die Kurve nach oben (in Richtung größerer y-Werte), ist b < 0 wandert sie nach unten (in Richtung kleinerer y-Werte).
Multiplikation von φ mit einer Zahl
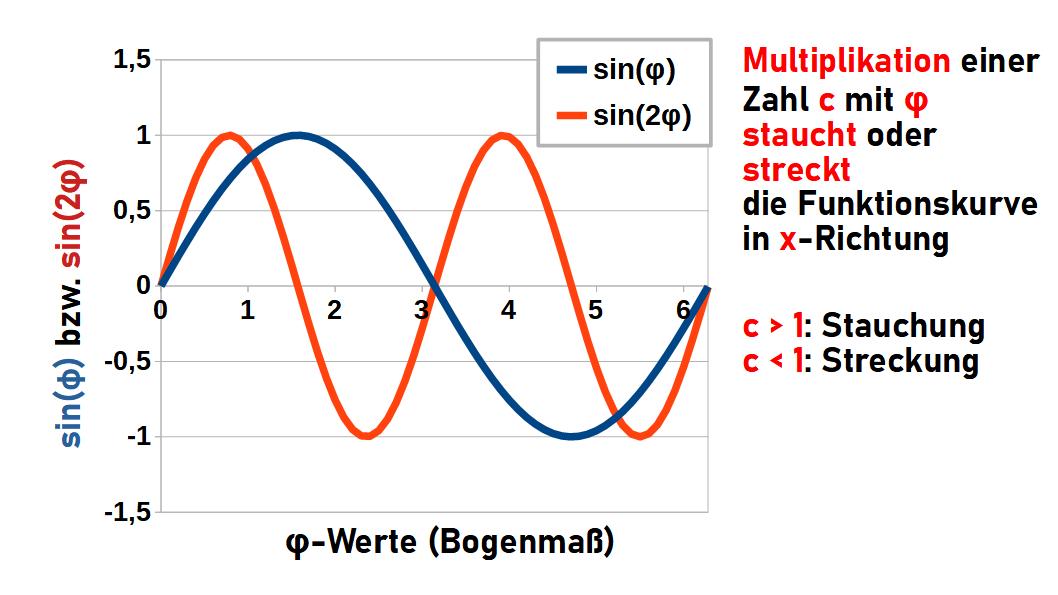
Bis jetzt haben wir uns Manipulationen der gesamten Sinus- oder Cosinusfunktion angeschaut. Jetzt geht es um die Multiplikation des Arguments der Sinus- bzw. Cosinusfunktion, sprich des Winkels φ, mit einem Faktor c: \(y=\sin{(c\cdot \varphi)}\).
Schauen wir uns als Beispiel \(y=\sin{(2\cdot \varphi})\) an.Wenn φ=2π ist, hat \(\sin{φ}\) den Wert \(\sin{2\pi}\). Dieser Wert ist für \(y=\sin{(2 \varphi})\) bereits bei φ=π erreicht. \(\sin{2\varphi}\) ändert sich also doppelt so schnell mit φ wie \(\sin{\varphi}\). Anders gesagt: die Funktionskurve ist in x-Richtung zusammengestaucht; zwischen 0 und 2π hat \(\sin{\varphi}\) jeweils ein Maximum bzw. Minimum, \(\sin{2\varphi}\) dagegen jeweils zwei!
Auch hier soll eine Animation den Einfluss der Konstanten c auf die Kurvenform erläutern.
Bei der Besprechung von Schwingungsvorgängen wird sich zeigen, dass dies einer höheren Frequenz einer Schwingung entspricht.
Addition einer Zahl zu φ
Statt φ mit einer Zahl zu multiplizieren, addieren bzw. subtrahieren wir jetzt eine Zahl d zum Winkel φ: \(y=\sin{(\varphi ± d)}\). Dies ändert nicht die Form der Kurve; es verschiebt sie aber um d in x-Richtung.
Man beachte: Wenn d subtrahiert wird, verschiebt sich die Kurve nach rechts! Entsprechend verschiebt sie sich nach links, wenn d addiert wird.
Wer möchte, kann sich dieses EXCEL-File mit einem Funktionsplotter herunterladen und darin mit frei wählbaren Werten für Amplitude, Frequenz, Phase und y-Offset der Sinusfunktion spielen. Nach Eingabe des x-Wertebereichs und der genannten Parameterwerte werden entsprechende Plots im Vergleich mit der einfachen Sinusfunktion generiert.
Komplexere Modifikationen
Es geht natürlich auch komplizierter. Zum Beispiel, indem man mehrere Basismodifikationen kombiniert und gleichzeitig Streckungen, Stauchungen und Verschiebungen in x- und y-Richtung durchführt.
Noch deutlich wilder geht es zu, wenn man keine konstanten, sondern sich mit φ verändernde Parameter zur Modifikation verwendet. Abb.8 zeigt sin(φ), multipliziert mit einer Amplitude, die exponentiell mit dem Winkel abfällt (\(a=e^{-0,2\cdot\varphi}\)). Wenn sich zusätzlich der Faktor vor φ mit dem Winkel ändert, variiert auch die Streckung oder Stauchung der Funktionskurve in x-Richtung. usw…
Der Phantasie sind kaum Grenzen gesetzt…
Beziehungen zwischen Sinus und Cosinus
Abb.3 zeigt bereits, dass sin(φ) und cos(φ) eng miteinander zusammenhängen. Verschiebt man die Kurve von cos(φ) um π/2 nach rechts, bekommt man die Kurve von sin(φ):\[\sin{(\varphi})=\cos{(\varphi-\pi/2})\](s. oben: Addition einer Zahl zu φ).
Der Tangens
Neben Sinus und Cosinus spielt die Tangensfunktion (abgekürzt: tan) eine wichtige Rolle in Mathematik und angewandter Wissenschaft.
Was ist der Tangens und warum ist er wichtig?
Seine Definition ist einfach: er ist definiert als das Längenverhältnis von Gegenkathete zu Ankathete (s. Abb.1) bzw. als Quotient von sin(φ) und cos(φ):\[tan(\varphi)=\frac{sin(\varphi)}{cos(\varphi)}\]Seine Wichtigkeit rührt daher, dass er die Steigung m einer Gerade y(x)=m·x+b angibt, die mit der x-Achse den Winkel φ einschließt.
Und Geraden spielen beispielsweise in der Differentialrechnung (Tangenten sind Geraden!) und bei vielen Methoden in den angewandten Wissenschaften (insbesondere der Physik) eine zentrale Rolle.
Die Funktionskurve des Tangens sieht völlig anders aus als die des Sinus oder Cosinus (Abb.9), ist aber auch periodisch. Er besitzt bei φ-Werten von π/2, 3π/2, 5π/2… eine Unendlichkeitsstelle. Bei Annäherung von links strebt der Tangens gegen +∞, bei Annäherung von rechts gegen -∞. In Abb.2 sieht man, dass beim Winkel π/2 die Länge der Ankathete 0 und die der Gegenkathete 1 beträgt, das Verhältnis also unendlich groß würde. Das Gleiche gilt für all anderen ungeraden Vielfachen von π/2.
Warum sind Sinus und Cosinus so wichtig?
Ganz am Anfang des Beitrags klang es schon mal an: Schwingungen und Wellen jeglicher Art sind – vor allem in den Naturwissenschaften und der Technik – praktisch überall zu finden. Stichworte sind Wasserwellen, Schallwellen, elektromagnetische Wellen, Wellenmechanik, Gravitationswellen etc. Und da die Bewegungen bei Schwingungen und Wellen periodisch sind, bieten sich Sinus und Cosinus für die mathematische Beschreibung solcher Vorgänge an.