Die Differentialrechnung spielt in Physik, Chemie und anderen quantitativen Wissenschaften eine zentrale Rolle. In diesem Beitrag soll ein erster Einblick in die Fragestellung, die grundlegenden Aspekte und Regeln der Differentialrechnung gegeben werden.
Wozu Differentielrechnung?
Die Differentialrechnung wurde von Isaac Newton und unabhängig davon Wilhelm Leibniz erfunden, um Probleme mit der Definition der Momentangeschwindigkeit zu lösen; sie hat ihren Ursprung also in der Physik.
Geschwindigkeit v ist definiert als der Quotient aus der Wegstrecke Δs, die während der Zeitspanne Δt zurück gelegt wird und eben dieser Zeitspanne: \[v=\frac{\Delta s}{\Delta t}\]
Sie stellt nach dieser Definition immer einen Mittelwert dar: Man misst die Wegstrecke Δs (z.B. 60 km) und die Zeitspanne Δt (z.B. 2 Stunden) und teilt die beiden durcheinander; v=30 km/h. Änderungen der Geschwindigkeit innerhalb Δt spielen bei dieser Rechnung keine Rolle; beispielsweise, ob man nach 20 km vor der Ampel abgebremst oder nach 40 km zum Überholen beschleunigt hat. Um Änderungen der Geschwindigkeit innerhalb Δt zu erfassen, muss Δt kleiner gemacht werden; je genauer man die Geschwindigkeit kennen will, desto kleiner muss Δt sein.
Idealerweise würde man Δt unendlich klein machen, also praktisch Null, und damit die Geschwindigkeit zu einem einzigen Zeitpunkt – die Momentangeschwindigkeit – erhalten. Allerdings kann man nicht durch Null teilen. Man ist also in der Zwickmühle, wenn man die Momentangeschwindigkeit ermitteln will.
Die Grundidee der Differentialrechnung
Die Differentialrechnung bietet einen Weg aus dieser Zwickmühle. Einen Weg, der erst mal ziemlich umständlich aussieht. Man definiert die Momentangeschwindigkeit zum Zeitpunkt t – also v(t) – als den Grenzwert des Quotienten aus Δs und Δt bei immer kleineren Werten für Δt.
\[v(t)=\lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t}\]
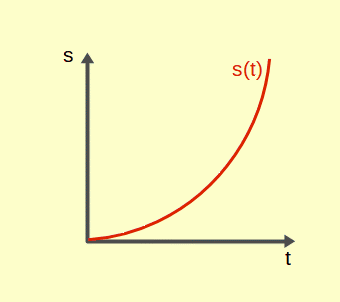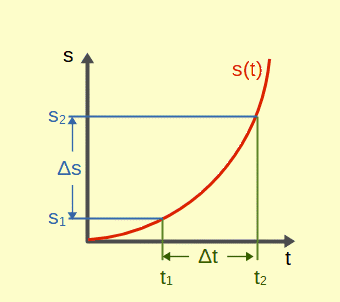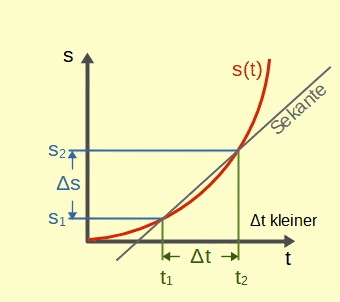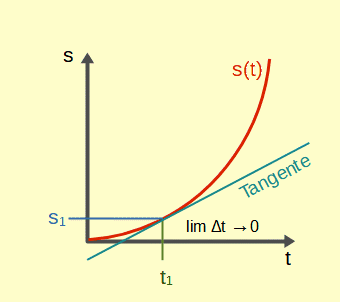
Wenn man die Wegstrecke gegen die Zeit in einem Graphen aufträgt, wird klar, dass dies dem Übergang von einer Sekante (eine Gerade, die die Kurve in zwei Punkten schneidet) zu einer Tangente (die Gerade, die die Kurve in einem Punkt nur berührt) entspricht.
Die Animation zeigt den Übergang von der Sekante in die Tangente im Punkt s1/t1, während Δt immer kleiner wird und zum Schluss gegen Null strebt. Die mittlere Geschwindigkeit während Δt entspricht der Steigung Δs/Δt der jeweiligen Sekante, die Momentangeschwindigkeit zur Zeit t1 der Steigung der Tangente. Eine nähere Betrachtung findet sich in einem speziellen Beitrag zum Thema Sekanten und Tangenten.
Δt kann man als Differenz
\[\Delta t = t_2 – t_1\]
schreiben. Oder aufgelöst nach t2:
\[t_2 = t_1+\Delta t\]
Entsprechendes gilt für Δs: \[\Delta s = s(t_2) – s(t_1)=\]\[s(t_1+\Delta t) – s(t_1)\]
Die Definition der Momentangeschwindigkeit kann also auch so geschrieben werden:
\[v(t_1)=\lim_{\Delta t \to 0} \frac{s(t_1+\Delta t) – s(t_1)}{\Delta t}\]
Oder wenn man statt t1 allgemeiner t schreibt:
\[v(t)=\lim_{\Delta t \to 0} \frac{s(t+\Delta t) – s(t)}{\Delta t}\]
Der geneigte Leser wird vielleicht sagen: „Aha, also tendenziell noch komplizierter als vorher…“
Doch das täuscht. Denn wenn man nicht mehr bei der allgemeinen Definition der Geschwindigkeit bleibt, sondern konkrete Funktionen s(t) betrachtet, kann man mit ein paar Tricks Δt im Nenner verschwinden lassen und so das Problem des „Teilen durch Null“ umgehen. Wir schauen uns dies am Beispiel s(t) = t² an.
\[v(t)=\lim_{\Delta t \to 0} \frac{s(t+\Delta t) – s(t)}{\Delta t}=\]
\[\lim_{\Delta t \to 0} \frac{(t+\Delta t)^2 – t^2}{\Delta t}=\]
\[\lim_{\Delta t \to 0} \frac{t^2+2 t \Delta t+(\Delta t)^2 – t^2}{\Delta t}=\]
\[\lim_{\Delta t \to 0} \frac{2 t \Delta t+(\Delta t)^2}{\Delta t}=\]
\[\lim_{\Delta t \to 0} 2 t+\Delta t=\]
\[2 t\]
Wir bekommen im Endeffekt: Wenn s(t) = t², dann ist die Momentangeschwindigkeit v(t) = 2t!
Wie schon gesagt: der Witz liegt darin, erst Δt im Nenner weg zu kürzen und danach den Übergang zu Δt=0 zu vollziehen.
Für viele einfache Funktionen der Wegstrecke s(t) hat man die entsprechenden Momentangeschwindigkeiten bereits ermittelt. Beispiele sind:
\(v(t)=0\)
c: Konstante, unabhängig von t
\(v(t)=1\)
\(v(t)=nt^{n-1}\)
n= reelle Zahl
\(v(t)=e^t\)
(e: Euler’sche Zahl: 2,718…)
s(t) und v(t) sind gleich!
\(v(t)=cos(t)\)
\(v(t)=-sin(t)\)
Im Interent kann man ausführliche Tabellen mit den Steigungen elementarer Funktionen finden.
Der Begriff der Ableitung
Doch die Differentialrechnung ist viel breiter anwendbar als nur zur Berechnung von Momentangeschwindigkeiten. Immer wenn ein funktionaler Zusammenhang f(x) besteht – also eine Abhängigkeit einer Größe f von einer anderen Größe x – stellt sich die Frage, wie stark sich f mit x ändert. f kann die Wegstrecke und x kann die Zeit sein, was unserer Diskussion der Momentangeschwindigkeit zugrunde liegt. Aber auch die Frage wieviel mehr Wein der Supermarkt kaufen muss, wenn sich die Zahl der Käufer ändert, um welchen Betrag der Luftdruck mit zunehmender Höhe fällt und wie stark die mittlere Welttemperatur in Abhängigkeit vom Kohlendioxid-Gehalt der Luft steigt kann mit Hilfe der Differentialrechnung bearbeitet werden.
Man spricht dann im Allgemeinen nicht von Momentangeschwindigkeit, sondern von der sog. Ableitung (die Momentangeschwindigkeit ist z.B. die Ableitung der Wegstrecke nach der Zeit), wobei es verschiedene Bezeichnungsweisen für eine Ableitung gibt:
f'(x) – gesprochen: f Strich von x – ist die kürzeste Schreibweise; \(\frac{df}{dx}\) – gesprochen: df nach dx – wird oft gebraucht, um die Nähe zum Mittelwert \(\frac{\Delta f}{\Delta x}\) zu betonen und wird Differentialquotient in Anlehnung an den Differenzenquotient genannt. Beide Bezeichnungen sind weit verbreitet.
Beide Schreibweisen sind auch geeignet, um höhere Ableitungen zu bezeichnen. Wir hatten gesehen, dass die Ableitung von s(t)=t² gleich 2t ist. Die Ableitung ist also immer noch von t abhängig und man kann sich fragen, wie groß die Änderung der Ableitung mit der Zeit ist. Man spricht dann von der zweiten Ableitung von s nach t und schreibt dafür
s“(t) oder \(\frac{d^2f}{dx^2}\)
gesprochen: s zweistrich von t bzw. d quadrat f nach dx quadrat.
Noch ein paar Anmerkungen zu den verschiedenen Schreibweisen für eine Ableitung:
Im Ausdruck \(f'(x)\) bedeutet der hochgestellte Strich, dass die Funktion \(f(x)\) nach x abgeleitet werden soll. Ein Ausdruck wie \(f’\) sagt gar nichts aus, solange nicht klar ist, nach welcher Variable abgeleitet werden soll. Er wird dennoch oft verwendet, wenn klar ist, dass es in der Funktion nur eine Variable (und nicht zwei, drei oder mehr) gibt und welche das ist.
Hätte man beispielsweise die Funktion \(t^2\cdot r\) wäre es unklar, ob t oder r die Funktionsvariable ist – oder ob beide Variablen sind. Erst die Formulierung \(f(r)=t^2\cdot r\) macht klar, dass r die Variable und t ein konstanter Parameter ist. Dann ist die erste Ableitung\[f'(r)=\frac{df}{dr}=t^2\]Was uns zur zweiten Schreibweise, dem Differentialquotienten, bringt.
Insbesondere in Anwendungen der Differentialrechnung wird häufig der Differentialquotient \(\frac{df}{dx}\) der Funktion \(f(x)\) benutzt. Denn mit den Differentialen \(dy\) und \(dx\) kann man in vielen Fällen rechnen. Außerdem macht er automatisch klar, was die Variable ist, nach der differenziert wird. Allerdings ist beim Rehnen Vorsicht geboten; denn Differentiale sind von der Definition her unendlich klein bzw. gehören zur Tangentialgeraden, nicht zur Funktion selbst.
Ein paar Beispiele sollen das illustrieren:
Die Gleichung\[\frac{dy}{dx}=y’\] kann nach dy aufgelöst werden:\[dy=y’\cdot dx\]Dass dies zulässig ist, kann man an der Definition von \(y’\) sehen. Der Differenzenquotient ist definiert als\[\frac{\Delta y}{\Delta x}=\frac{y(x+\Delta x)-y(x)}{\Delta x}\]\(\Delta y\) und \(\Delta x\) sind endliche Differenzen, mit denen man unbedenklich rechnen kann. Multiplikation mit \(\Delta x\) ergibt\[\Delta y=\frac{y(x+\Delta x)-y(x)}{\Delta x}\cdot \Delta x\]Beim Übergang \(\Delta x\) gegen Null wird der Bruch zur Ableitung \(y’\) und dei Differenzen werden zu den Differentialen.
Dagegen ist ein Ausdruck wie \(\frac{y‘}{dx}\) nicht erlaubt. Denn\[\frac{\Delta y}{\Delta x^2}=\frac{1}{\Delta x}\frac{\Delta y}{\Delta x}\]Beim Übergang \(\Delta x\) gegen Null wird der Bruch zwar zur Ableitung \(y’\), aber \(\Delta x\) bleibt im Nenner stehen und wird unendlich klein, was verboten ist.
Zusammenfassung
- Mit der Differentialrechnung kann man die Steigung einer Funktion f(x) in einem Punkt berechnen.
- Dazu wird der Differenzenquotient Δf/Δx durch den Grenzübergang zu Δx=0 in den Differenzialquotienten df/dx überführt.
- Der Differenzialquotient df/dx wird auch als Ableitung der Funktion f(x) bezeichnet.
- Dies entspricht geometrisch dem Übergang von einer Sekante zur Tangente an der Kurve.
- Ableitungen können nach wie vor von der unabhängigen Variablen x abhängen; sie können selbst weiter abgeleitet (differenziert) werden (die Ableitung der Momentangeschwindigkeit nennt man z.B. Beschleunigung).
- Für elementare Funktionen wurden die Ableitungen bereits bestimmt und in Tabellen gelistet.