Um was geht es?
Die Grundlagen von Funktionen in der Mathematik und einige elementare Funktionen haben wir in anderen Beiträgen bereits beschrieben.
Jetzt geht es um die generelle Charakterisierung von Funktionen – also um Eigenschaften, mit denen Funktionen in Kategorien eingeteilt werden:
Diskrete/kontinuierliche Funktionen
Schon in der Einführung in den Funktionsbegriff hatten wir gesehen, dass manche Funktionen nur als Tabelle, andere mit Hilfe einer Funktionsgleichung dargestellt werden können.
Wenn die Funktion y=y(x) aus einer Tabelle besteht, gibt es nur für einige x-Werte einen y-Wert. Die x-Werte machen Sprünge; es handelt sich um diskrete x-Werte (Abb. 1).
Dagegen kann man in eine Funktionsgleichung beliebige x-Werte einsetzen – zumindest solange, wie sie aus der Definitionsmenge stammen. Im Falle der reellen Zahlen als Definitionsmenge bedeutet dies, dass die x-Werte beliebig nah beieinander liegen. Man bekommt eine kontinuierliche Funktion (keine Lücken im Funktionsgraph; Abb. 2). Gleiches gilt für irgendwelche zusammen hängende Intervalle der reellen Zahlen als Definitionsmenge (z.B. die positiven reellen Zahlen).
Für die Funktionsgraphen bedeutet das: diskrete Funktionen bestehen aus einzelnen, getrennten Punkten; kontinuierlliche Funktionen aus durchgezogenen Linien bzw. Kurven.
Monoton steigende/fallende Funktionen
Funktionen, die mit steigenden x nur ansteigende oder abfallende y-Werte aufweisen, kommen in vielen Wissenschaften vor. Sie haben die Besonderheit, dass aus ihnen eine Umkehrfunktion über den gesamten Wertebereich gebildet werden kann. Umkehrfunktionen werden in einem eigenen Beitrag besprochen.
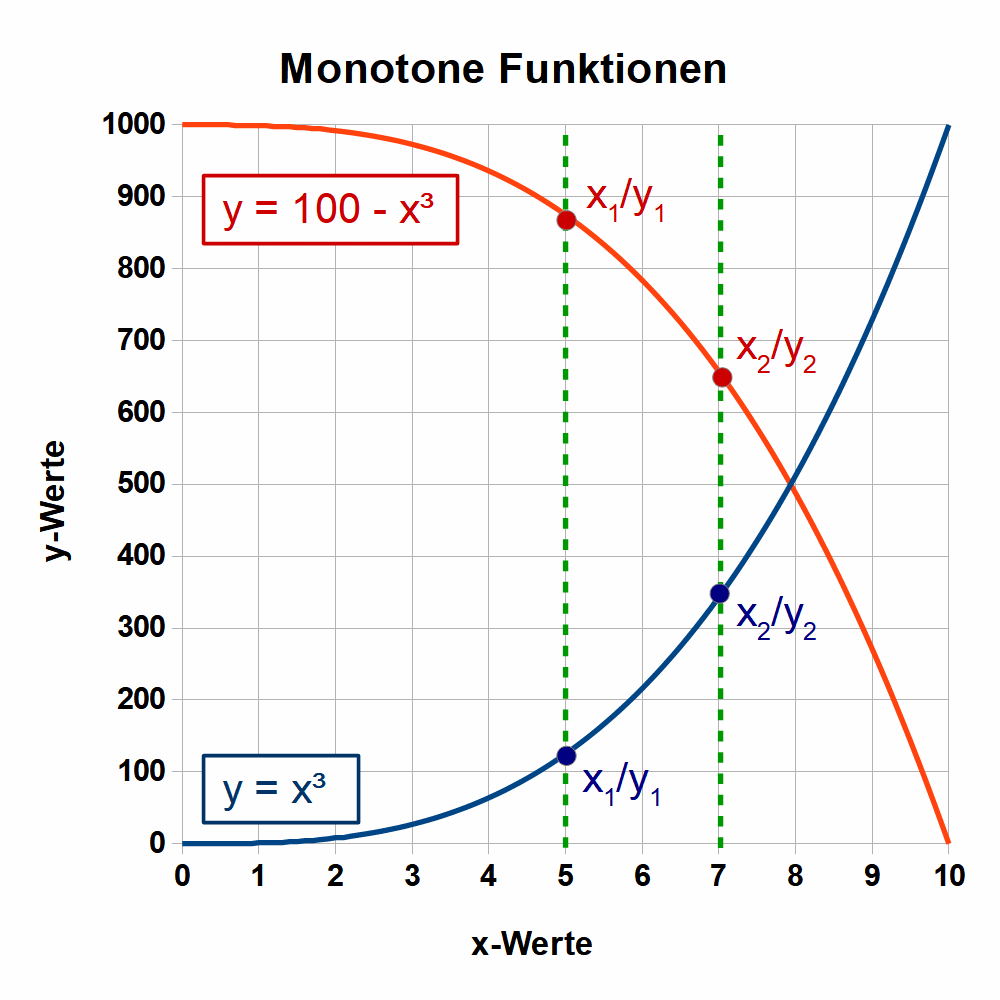
Solche Funktionen haben weder Maxima noch Minima – außer am Rand ihres Definitionsbereichs. Man spricht von streng monoton steigenden oder fallenden Funktionen. Abb.3 zeigt für x≥0 eine streng fallende (rot) und eine streng steigende (blau) Funktion.
- streng monoton steigend:
wenn x1 < x2 dann y1 < y2 - streng monoton fallend:
wenn x1 < x2 dann y1 > y2
Wir haben dabei die Abkürzung y1 für y(x1) benutzt. Dürfen die beiden y-Werte auch gleich sein, so sind die Funktionen nicht mehr streng fallend oder steigend.
- monoton steigend:
wenn x1 < x2 dann y1 ≤ y2 - monoton fallend:
wenn x1 < x2 dann y1 ≥ y2
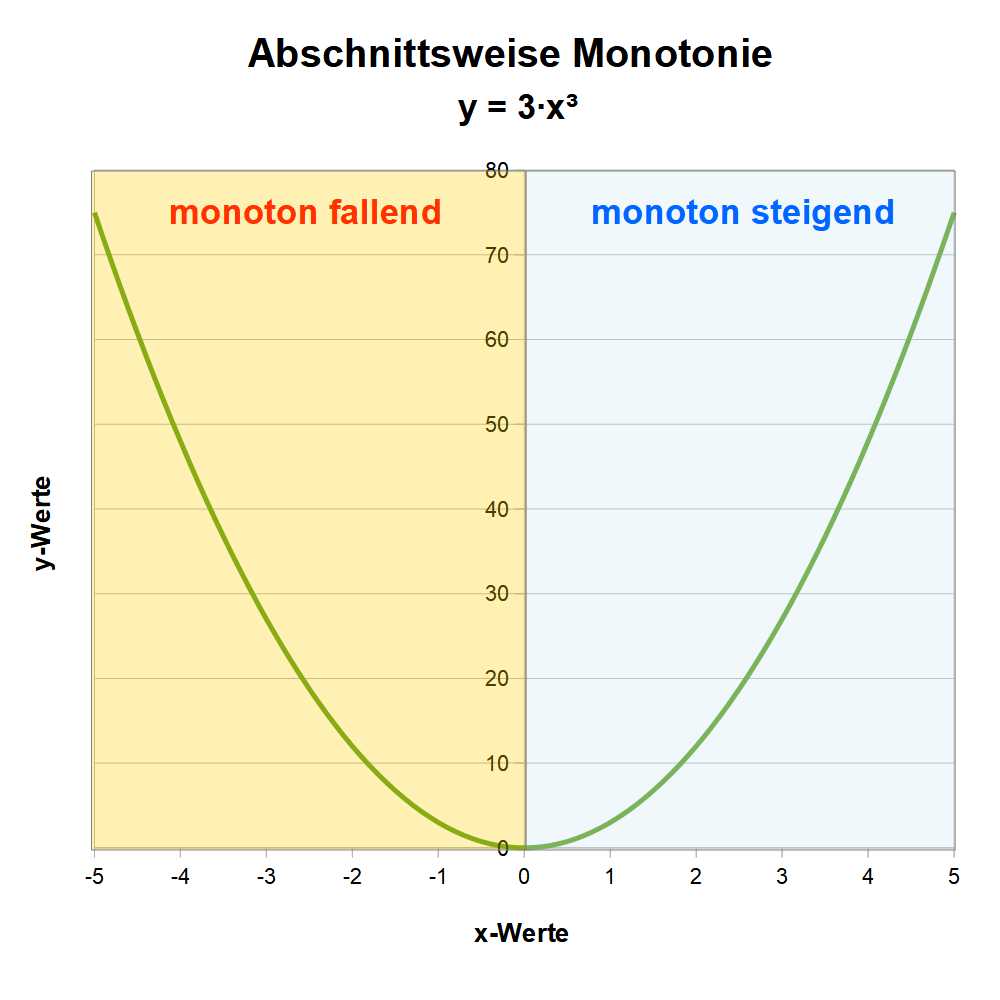
Viele Funktionen steigen oder fallen allerdings nur in bestimmten Abschnitten der x-Werte (in bestimmten Intervallen der Definitionsmenge). Sie haben dann Minima oder Maxima der Funktionswerte, bei denen eine steigende in eine fallende Funktionskurve übergeht – oder umgekehrt. Man spricht dann von einer abschnittsweisen Monotonie der Funktion (Abb. 4).
In diesem Beispiel ist die Funktion y = 3x² bei x-Werten im Intervall [0,∞], also bei x ≥ 0, (streng) monoton steigend, im Intervall [-∞,0] dagegen (streng) monoton fallend. Bei x = 0 hat die Funktion ein Minimum: sie geht hier vom fallenden in den steigenden Abschnitt über.
Gerade/ungerade Funktionen
Unter den vielen denkbaren Funktionen gibt es solche, die besondere Symmetrieeigenschaften besitzen. Besonders wichtig sind sog. gerade bzw. ungerade Funktionen – die trigonometrischen Funktionen Sinus (ungerade) und Cosinus (gerade) sind wichtige Beispiele. Weiß man, dass eine Funktion gerade oder ungerade ist, werden viele Berechnungen einfacher, was bei der Anwendung von Funktionen in den Wissenschaften vorteilhaft ist.
Doch was heißt gerade und ungerade?
Gerade Funktionen
Funktionen f(x) sind dann gerade, wenn
f(x) = f(-x)
d.h. der Funktionswert ist unabhängig vom Vorzeichen des x-Wertes. Ein Beispiel ist die Funktion y = x². Ersetzt man x durch -x, so ergibt sich der y-Wert zu
y(-x) = (-x)² = (-1)²x² = x² = y(x)
Im Funktionsgraphen zeigt sich das dadurch, dass die Funktionskurve symmetrisch zur y-Achse ist (Video 1). Diese Achssymmetrie ist übrigens äquivalent zu einer 180°-Drehung der Funktionskurve um die y-Achse.
Video 1: y=x² als Beispiel einer geraden Funktion
Ungerade Funktionen
Funktionen f(x) sind dann ungerade, wenn
f(x) = -f(-x)
d.h. der Funktionswert kehrt sein Vorzeichen um, wenn der x-Werte sein Vorzeichen umkehrt. Ein Beispiel ist die Funktion y = x³. Ersetzt man x durch -x, so ergibt sich der y-Wert zu
y(-x) = (-x)³ = (-1)³x³ = -x³ = -y(x)
Im Funktionsgraphen zeigt sich das dadurch, dass die Funktionskurve symmetrisch zum Ursprung des Koordinatensystems ist (Video 2).
Video 2: y=x³ als Beispiel einer ungeraden Funktion
Periodische Funktionen
Es gibt Funktionen, deren Funktionswerte sich bei gleichem x-Abstand wiederholen; oder als Formel:
f(x+a) = f(x)
wobei a einen konstanten Wert hat und Periode genannt wird. Wenn man also von einem beliebigen x-Wert zu dem um a größeren Wert übergeht, bleibt der Funktionswert gleich.
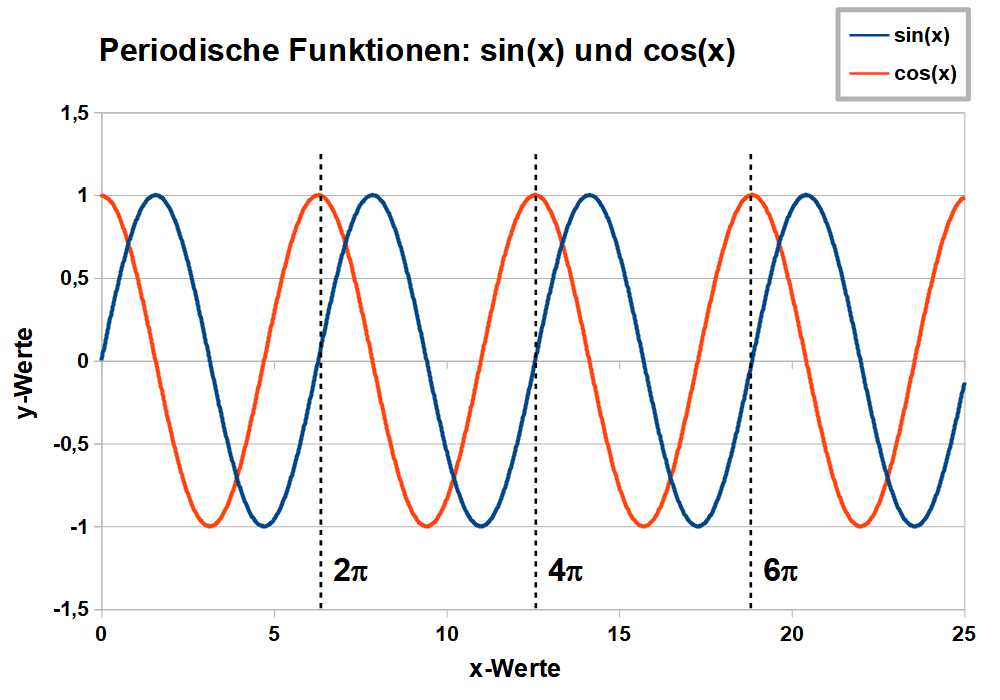
Die trigonometrischen Funktionen Sinus und Cosinus sind die wichtigsten Beispiele für periodische Funktionen. sin(x) und cos(x) haben beispielsweise eine Periode von 2π (Abb.5). Übrigens: Alle periodischen Funktionen lassen sich aus Sinus- und Cosinusfunktionen durch sog. Linearkombinationen zusammenbauen. Dies spielt in vielen Anwendungen eine überragende Rolle (Stichwort: Fourier-Reihen).
Implizite/explizite Funktionen
Was ist das denn schon wieder? Hört sich kompliziert an, ist aber ganz einfach.
Eigentlich geht es nur um Schreibweisen. y = y(x) ist die explizite Schreibweise der Funktionsgleichung; denn es wird jedem x-Wert direkt (explizit) ein y-Wert zugeordnet. Man kann aber die Formel für die x-Abhängigkeit auch auf die linke Seite der Gleichung bringen:
y – y(x) = 0
Und schon haben wir die implizite Funktionsgleichung. Das wird besser verständlich an einem Beispiel:
- explizite Funktion:
y = 3x + 5 - implizite Funktion:
y – 3x – 5 = 0
Die implizite Form der Funktionsgleichung scheint nur eine Spielerei zu sein. Sie hat jedoch für viele Anwendungen Vorteile, bei denen die sog. Differentialrechnung eine Rolle spielt. Außerdem betont sie die Gleichwertigkeit der beiden Variablen; denn sie lässt offen, welche die abhängige bzw. die unabhängige ist.
Stetigkeit
Anschaulich gesprochen bedeutet Stetigkeit, dass man Funktionskurven in einem Rutsch ohne Abheben eines Zeichenstifts nachzeichnen kann, solange sich ihre unabhängige Variable im Definitionsbereich befindet. Bei vielen Funktionen ist das für den ganzen Definitionsbereich gegeben. y = x², y = ex oder sin(x) sind solche Beispiele. Diese Funktionen sind für alle reele Zahlen x definiert (die Funktionsgraphen können im Beitrag Elementare Funktionen bewundert werden).
In der Mathematik muss die Vorschrift „in einem Rutsch zeichnen“ allerdings präzisiert werden. Denn es gibt Funktionen, bei denen man auf den ersten Blick nicht entscheiden kann, ob der Bleistift abgehoben werden muss.
Zunächst muss betont werden, dass sich Steigkeit immer auf einen einzigen Wert der Definitionsmenge bezieht. Erst wenn alle Werte der Definitionsmenge stetig sind, kann man von einer im Ganzen stetigen Funktion sprechen.
Eine Funktion ist an der Stelle x0 stetig, wenn mit einem immer stärkeren Näherrücken des x-Wertes an x0 heran gleichzeitig der y-Wert sich dem Wert y0 = y(x0) nähert. Oder anders gesagt: wenn x von x0 nur sehr wenig abweicht, weicht auch y von y0 nur sehr wenig ab. Oder in mathematischer Sprache:
Wenn |x – x0| immer kleiner wird, wird auch |y – y0| immer kleiner.
„| … |“ bedeutet, dass der Absolutbetrag der Differenz gemeint ist, dass also das Vorzeichen der Differenz weggelassen wird; Beispiel: |5-2| = |2-5| = 3.
Sind Funktionen an der Stelle x0 nicht stetig, liegt meist entweder ein Sprung oder eine Unendlichkeitsstelle vor. Im Detail kann die Stetigkeitsfrage in solchen Fällen recht schwierig werden. Das sind aber Spezialfälle, die hier nicht behandelt werden sollen. Wer will kann auf mathebibel.de mehr und Exakteres zur Frage der Stetigkeit finden.
Minima, Maxima, Wendepunkte
Für die Bewertung einer Funktion ist es wichtig, ob sie über Minima und/oder Maxima verfügt. Minima und Maxima werden unter dem Begriff „Extrema“ zusammengefasst. Ein Minimum an der Stelle \(x_0\) ist dadurch gekennzeichnet, das in der Umgebung von \(x_0\) alle Funktionswerte größer als \(f(x_0)\) sind. Dem entsprechend liegt ein Maximum bei \(x_0\) vor, wenn die Funktionswerte in der Umgebung von \(x_0\) kleiner als \(f(x_0)\) sind.
Man unterscheidet lokale von absoluten Minima bzw. Maxima. Eine Funktion kann mehrere Minima (Maxima) haben. Das Minimum mit dem kleinsten (größten) Funktionswert ist das absolute Minimum (Maximum).
In einem Minimum geht bei steigendem x-Wert ein streng monoton fallender in einen streng monoton steigenden Funktionsabschnitt über (salopp gesagt: die Funktionskurve dreht um). Bei einem Maximum ist es umgekehrt. Im Minimum bzw. Maximum selbst ist die Steigung der Funktionskurve Null.
Interessanterweise gibt es aber auch den Fall, dass die Funktion an der Stelle \(x_0\) die Steigung Null erreicht, dann aber weiter macht wie bisher. Man spricht von einem Wendepunkt; die Funktion ist rechts und links vom Wendepunkt monoton steigend bzw. fallend.
Beispiele: Die Funktion \(f(x)=x^2\) hat an der Stelle \(x_0=0\) ein Minimum, die Funktion \(f(x)=-x^2\) hat dort ein Maximum und die Funktion \(f(x)=x^3\) einen Wendepunkt. Die Funktion \(g(x)=-x^3\) entspricht der an der x-Achse gespiegelten Funktion \(f(x)=x^3\); sie ist links und rechts vom Wendepunkt monoton fallend. Am einfachsten macht man sich all das an Funktionsgraphen klar.
Was bleiben soll...
- Gerade bzw. ungerade Funktionen f(x) liegen vor, wenn gilt: \(f(x)=f(-x)\) bzw.\(f(x)=-f(-x)\).
- Abschnitte von Funktionen f(x), in denen der Funktionswert mit x ununterbrochen ansteigt (abfällt), heißen monoton steigend (fallend).
- Bei periodischen Funktionen f(x) wiederholt sich der Funktionsverlauf in regelmäßigen Abständen a: \(f(x)=f(x+a)\).
- Funktionen können in expliziter (\(y=f(x)\)) oder impliziter (\(y-f(x)=0\)) Form vorkommen.
- Eine Funktion f(x) ist an der Stelle \(x_0 \) stetig, wenn der Funktionswert dort keine Sprünge macht („ein Zeichenstift muss beim Nachfahren der Funktionskurve nicht angehoben werden“).
- Eine Funktion \(f(x)\) kann Maxima, Minima (zusammenfassend Extrema genannt) oder Wendepunkte haben; bei einem Minimum geht mit steigendem x eine fallende Funktionskurve in eine steigende über, beim Maximum ist es umgekehrt. Beim Wendepunkt bleibt die Monotonie der Funktion enhalten. Die Steigung der Funktionskurve ist bei beiden Extrema und beim Wendepunkt Null.
Ausblick
Mit dem Wissen aus dem vorliegenden Beitrag und den Grundlagen von Funktionen können die Eigenschaften der elementaren Funktionen vorgestellt und diskutiert werden. Diese sehr einfachen Funktionen sind die Bausteine, aus denen sich eine Vielzahl komplexerer Funktionen zusammensetzt. Den Trigonometrischen Funktionen ist aufgrund ihrer besonderen Bedeutung ein eigener Beitrag gewidmet.