In einer Reihe von Beiträgen werden verschiedene Aspekte der Differentialrechnung beleuchtet (Diffentialrechnung – ein Überblick; Diffentialrechnung: Sekanten, Tangenten, Differenzen- und Differentialquotient; Diffentialrechnung: Produktregel und Kettenregel; Stetigkeit und Differenzierbarkeit).
Jetzt sollen ein paar Beispiele für die Anwendung der Differentiationsregeln gezeigt werden, um sich an ihre Anwendung ein wenig gewöhnen zu können und Anregungen für die Beschäftigung mit Übungsaufgaben, die im Internet und anderswo in Fülle zu finden sind, zu geben.
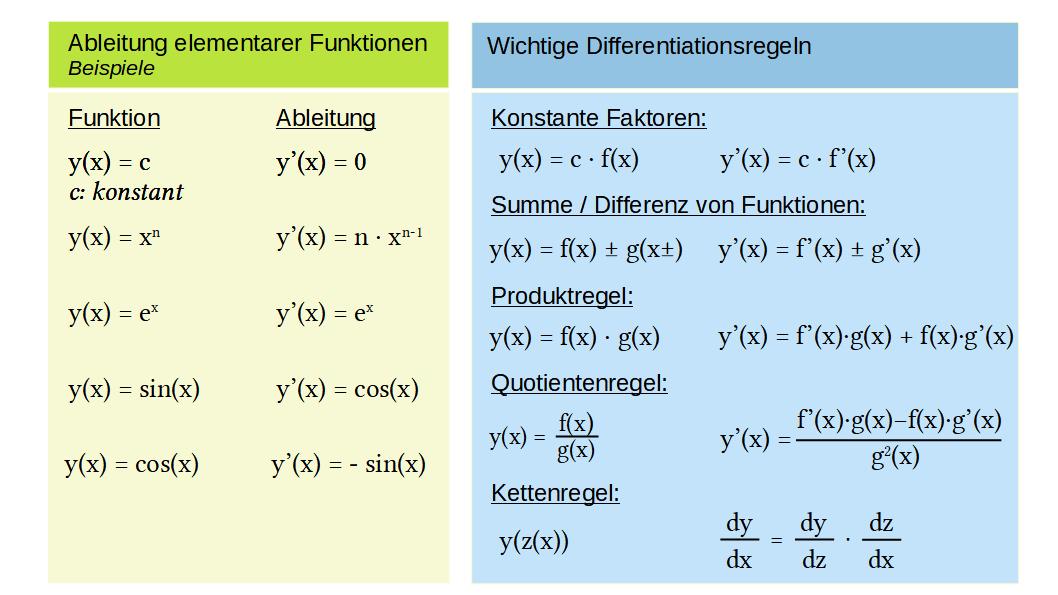
Ableitungen von elementaren Funktionen und Differentiationsregeln
Im Folgenden werden wir die Ableitungen einiger elementarer Funktionen und wichtige allgemeine Differentiationsregeln benötigen. Deshalb zur Erinnerung in Abb.1 eine kurze Liste.
Beispiele für Differentiationen
Geschwindigkeit und Beschleunigung
Eine konstant beschleunigte Bewegung wird in der Physik mit folgender Formel berechnet:
\[s(t)=s_0+v_0 \cdot t+\frac{1}{2} \cdot a \cdot t^2\]
s ist die zurück gelegte Strecke und t ist die Zeit. \(s_0\) und \(v_0\) sind Anfangsstrecke und Anfangsgeschwindigkeit zur Zeit t=0 und a ist eine weitere Konstante. Ein Stein, der im Schwerefeld der Erde zu Boden fällt, gehorcht zum Beispiel diesem Gesetz. Die Ableitung nach der Zeit ergibt die Geschwindigkeit v zur Zeit t:
\[v(t)=s'(t)=v_0+a \cdot t\]
\(s_0\) ist konstant und fällt bei der Ableitung fort. Die Ableitung von t ist 1; es bleibt die konstante Anfangsgeschwindigkeit \(v_0\) als Vorfaktor stehen. Und \(t^2\) ergibt abgeleitet \(2 \cdot t\); die 2 kürzt sich weg und a bleibt übrig.
Leitet man v(t) wieder nach t ab, ergibt sich
\[v'(t)=s^{\prime\prime}(t)=a\]
v'(t) ist die Änderungsrate der Geschwindigkeit, also die Beschleunigung, womit auch klar ist, was a bedeutet…
Gedämpfte Schwingung
Schwingungen sind in der Physik von besonderer Bedeutung. Und nicht nur dort…
In der Realität sind Schwingungen immer gedämpft: sie gehen nicht ewig weiter, sondern klingen langsam ab. Schwingungen werden mathematisch mit Sinus- oder Cosinusfunktionen beschrieben. Und das Abklingverhalten kann mit der Exponentialfunktion simuliert werden. Schauen wir uns die Schwingung sin(2πt) an, die mit der einfachen Exponentialfunktion e-t gedämpft wird. Dann gilt für die Auslenkung der Schwingung
\[y(t)=e^{-t} \cdot \sin(2 \cdot \pi \cdot t)\]
Die Ableitung ist ein wenig kompliziert und erfordert u.a. die Anwendung der Produkt- und Kettenregel. Legen wir los:
Wir haben das Produkt zweier Funktionen: \(e^{-t}\) und \(\sin(2 \cdot \pi \cdot t)\). Man muss also die Produktregel anwenden, für die man die Ableitung beider Funktionen nach t kennen muss. \(e^{-t}\) wäre einfach, wenn nicht das Minuszeichen im Exponenten stünde. Deshalb braucht man die Kettenregel. (-t) nach t abgeleitet ergibt (-1), was zur Ableitung \(-e^{-t}\) führt.
Die Sinusfunktion muss ebenfalls mit der Kettenregel abgeleitet werden. Wenn man \(z(t)=2 \cdot \pi \cdot t\) setzt, bekommt man \(z'(t)=2 \cdot \pi\). Wir haben also:
\(\frac{d(e^{-t})}{dt}=-e^{-t}\) und \(\frac{d(\sin(2 \cdot \pi \cdot t))}{dt}=2 \cdot \pi \cdot \cos(2 \cdot \pi \cdot t)\)
Einsetzen in die Produktregel gibt:
\[y'(t)=e^{-t} \cdot 2 \cdot \pi \cdot \cos(2 \cdot \pi \cdot t)-e^{-t} \cdot \sin(2 \cdot \pi \cdot t)\]
Schön kompliziert. Schauen wir uns den Funktionsverlauf von y(t) und y'(t) an:
Die blaue Kurve y(t) ist schwingt mit konstanter Frequenz auf und ab, wobei die Amplitude (der Ausschlag nach oben und unten) immer kleiner wird. Dadurch nimmt die Steigung y'(t) der Sinuskurve ebenfalls ab.
Die Änderungsrate ist am kleinsten bzw. größten, wenn y(t) die x-Achse kreuzt, also Null ist. Und die Änderungsrate ist Null, wenn y(t) minimal oder maximal ist.

Anwendung der Quotientenregel
Im Beitrag Differentialrechnung: Produktregel und Kettenregel wurde bewiesen, dass die Ableitung von \(y(x)=x^n\) lautet \(y'(x)=n \cdot x^{n-1}\), wobei n eine natürliche Zahl oder ein Bruch sein kann. Es stellt sich die Frage, was bei einem negativen Exponenten geschieht. Beginnen wir mit \(y(x)=x^{-1}=\frac{1}{x}\).
Identifiziert man die 1 im Zähler mit f(x) und x im Nenner mit g(x) in der Quotientenregel dann ergibt sich\[y'(x)=\frac{(1)^{\prime} \cdot x-1 \cdot x^{\prime}}{x^2}\] Da 1 abgeleitet Null und x abgeleitet 1 ergibt, folgt \[y'(x)=-\frac{1}{x^2}=-x^{-2}\] In diesem Fall stimmt die Differentiationsregel für \(x^n\) nach wie vor.
Wie schaut es mit höheren negativen Potenzen aus? Dazu wenden wir die Kettenregel auf \[y(x)=x^{-p}=\frac{1}{x^p}\] an. Wir setzen \(z(x)=x^p\) und erhalten \(y(z)=z^{-1}\). Die Ableitung von y(z) nach z haben wird eben ermittelt: \[\frac{dy}{dz}=-z^{-2}\] Und die Ableitung von z nach x lautet \[\frac{dz}{dx}=p \cdot x^{p-1}\] Einsetzen in die Kettenregel gibt \[\frac{dy}{dx}=\frac{dy}{dz} \cdot \frac{dz}{dx}=-z^{-2} \cdot p \cdot x^{p-1}\] Einsetzen von z(x) ergibt \[\frac{dy}{dx}=-x^{p^{-2}} \cdot p \cdot x^{p-1}\] Anwendung der Rechenregeln für Potenzen führt zu \[\frac{dy}{dx}=-p \cdot x^{-2 \cdot p } \cdot x^{p-1}=-p \cdot x^{-2 \cdot p+(p-1)}\] was schließlich \[\frac{dy}{dx}=-p \cdot x^{-p-1}\] ergibt.
Die Ableitungsregel für \(y(x)=x^n\) ist also auch für negative Exponenten erfüllt: n wird zum Vorfaktor und der Exponent wird um 1 erniedrigt! Die Ableitungsregel für \(y(x)=x^n\) gilt also für alle rationalen Zahlen für n.
Aufgabensammlungen
Um die Differentialrechnung wirklich zu beherrschen, gilt wie fast immer: üben, üben, üben…
Im Internet gibt es viele Seiten mit Aufgabensammlungen zur Differentialrechnung, mit denen man Erfahrungen im Differenzieren sammeln kann. Hier nur zwei Beispiele:
- 123mathe.de
- Universität Wien (umfangreich, auch fortgeschrittene Aufgabenstellungen)